Exercice geométrie 2 nd ...

par **coco_59n** » 06 Jan 2007, 12:24

bonjour, j'ai un exercice où j'ai des doutes :

la figure : http://www.hiboox.com/image.php?img=45c8b2d6.jpg

ABCD est un carré de coté 15 et AKIJ un carré de coté x non nul

1) Exprimer en fonction de x l'aire totale de la partie hachurée

J'ai donc calculé aire AKIJ + aire DCI mais je ne suis pas sur du tout de mes calculs intermédiaires, si quelqu'un pouvez m'aider pour comparer de le resultat final....

je trouve 3x²/2+14x/2+112.5

merci d'avance

par **yggdrasiil** » 06 Jan 2007, 12:52

Je n'arrive pas au même résultat que toi.

L'aire totale vaut effectivement aire(AJIK) + aire(DCI).

aire(AJIK) =

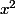
aire(DCI) =

après simplification.

D'où l'aire totale :

Donne-nous peut-être tes calculs, ça serait plus simple pour comparer.

par **coco_59n** » 06 Jan 2007, 12:58

Pour AKIJ c'est bon pour moi,

Mais pour DIC comment as tu procéder, moi : aire DIC = aire ADC - ( aire AJI + aire JID )

par **coco_59n** » 06 Jan 2007, 13:46

quelqu'un pour m'aider svp?? merci

par **coco_59n** » 06 Jan 2007, 14:09

??????????????????????

par **coco_59n** » 06 Jan 2007, 14:25

à voila, je croi que j'i trouvé ton raisonnement,

ensuite, il faut determiner x pour que l'aire hachurée soit égale à l'aire non hachurée

aire partie hachurée : x²-15/2x+225/2

par **coco_59n** » 06 Jan 2007, 14:36

svp aidez moi !!!!!!

merci d'avance

par **yggdrasiil** » 06 Jan 2007, 14:37

coco_59n a écrit:x²-15/2x+225/2

Non. La façon dont tu calcules l'aire de DCI est correcte, mais pas la réponse.

La bonne réponse est :

par **yggdrasiil** » 06 Jan 2007, 14:39

coco_59n a écrit:svp aidez moi !!!!!!

merci d'avance

Mais qu'elle impatience, laisse-nous le temps de répondre. Et imagine bien qu'on ne passe pas notre temps à répondre à des questions de math sur les forums. On a aussi des activités à côté !

par **coco_59n** » 06 Jan 2007, 15:33

oui désolé pour mon impatience^^

2) determiner x pour que l'aire hachurée soit egale à l'aire non hachurée.

merci yggdrasil pour la question 1

par **yggdrasiil** » 06 Jan 2007, 16:56

coco_59n a écrit:2) determiner x pour que l'aire hachurée soit egale à l'aire non hachurée.

Ca veut dire que l'équation que tu as trouvé en 1) aura comme résultat La moitié de l'aire totale, ie

.

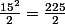
Tu poses ton équation :

.
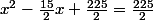
Tu simplifies :

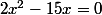
et tu résouts cette équation pour

.
Évidemment, seule une des deux solutions sera la bonne. Cela tombe sous le sens dans ce cas.

Exercice geométrie 2 nd ...

exercice geométrie 2 nd ...

Qui est en ligne