toulousaine313131 a écrit:j'ai un probléme parce que avec les 2 methodes à chaque fois je trouve IK= a mais c'est pas possible je fait:
AC= a+a = 2a donc IJ= a
et
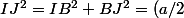^2+(a/2)^2=a/2+a/2=a)
Non, si tu as bien fait ta figure, tu devrais te retrouver avec un cube en perspective cavalière dont la face du dessus est ABCD (A au sommet à gauche et B immédiatement à droite).
La face en dessous est EFGH avec E en bas à gauche et F qui suit immédiatement à droite.
La face face à toi est donc ABFE en tournant du sommet à gauche dans le sens des aiguilles d'une montre.
Bref, une fois que c'est plus clair, on va y arriver.
Représente la face ABCD en 2D. C'est un carré. Que vaut la longueur AC sachant que AB=a et BC=a ?
Sans doute pas 2a ! Il faut utiliser Pythagore ici, encore une fois, et tu verras la différence. Aussi, tu as bien fait d'utiliser Thalès pour montrer que IJ=(1/2)*AC mais c'est se compliquer la vie pour rien.
Tu pouvais tout autant calculer IJ grâce à Pythagore en posant IB=BJ=a/2...
Pourquoi n'appliques-tu pas ce qu'on te dit ? Je t'ai pourtant donné la réponse un peu plus haut.
