Exercice de géométrie 2de...

[valorisa]

Bonjour,

Voici l'énoncé de l'exercice : " Sur chacun des trois côtés d'un triangle rectangle d'hypoténuse 4, on construit extérieurement trois triangles équilatéraux. Quelle est la somme des aires de ces trois triangles ?? "

J'ai bien trouvé l'aire du triangle équilatéral (A'BC) (lequel a pour base l'hypoténuse du triangle rectangle) qui est égale à mais le théorème de Pythagore ne me donne rien de parlant pour aller plus loin et trouver les aires des 2 autres triangles équilatéraux.

http://nsa33.casimages.com/img/2013/10/07/131007010226801121.jpg

Merci d'avance à toute personne qui me fera avancer là où je bloque.

Valorisa

[WillyCagnes]

bonjour,

soit a et b les cotés opposés à C l'hypothenus
triangle rectangle entraine a²+b²=c² =16

calcul des surfaces des triangles externes
coté hypothenus =
coté a =
coté b =

doù la somme des 3 triangles externes =
avec a²+b²=c²

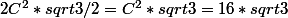
[valorisa]

Merci WillyCagnes pour la réponse mais pourriez-vous, s'il vous plaît, détailler un peu plus votre réponse ? Là je suis pour le moment un peu perplexe au sujet de la détermination de l'égalité des côtés a, b et C. Comment trouvez-vous ces résultats de façon plus décomposée ?

Merci d'avance.

Valorisa

[coote]

Merci WillyCagnes pour la réponse mais pourriez-vous, s'il vous plaît, détailler un peu plus votre réponse ? Là je suis pour le moment un peu perplexe au sujet de la détermination de l'égalité des côtés a, b et C. Comment trouvez-vous ces résultats de façon plus décomposée ?

Merci d'avance.

Valorisa

bonjour

il veux dire :

aire du triangle de cote a =
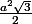
et ainsi de suite ...

[valorisa]

bonjour

il veux dire :

aire du triangle de cote a =
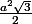
et ainsi de suite ...

Bonsoir,

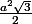
J'ai bien compris que a = mais c'est la manière d'y arriver qui m'intéresse.

Valorisa

[coote]

Bonsoir,

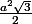
J'ai bien compris que a = mais c'est la manière d'y arriver qui m'intéresse.

Valorisa

bon, par la même manière que tu a utilise pour trouver l'aire de triangle de cote 4

[valorisa]

bonjour,

soit a et b les cotés opposés à C l'hypothenus
triangle rectangle entraine a²+b²=c² =16

calcul des surfaces des triangles externes
coté hypothenus =
coté a =
coté b =

doù la somme des 3 triangles externes =
avec a²+b²=c²

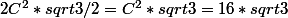
Il me semble que l'aire du triangle équilatéral est :

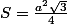
mais je peux me tromper.

Donc ce ne serait pas plutôt ?

coté hypoténuse =
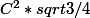
coté a =
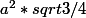
coté b =

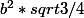
[coote]

Il me semble que l'aire du triangle équilatéral est :

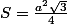
mais je peux me tromper.

oui c'est bien ca

[valorisa]

oui c'est bien ca

coté hypoténuse =
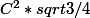
coté a =
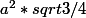
coté b =

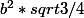
[coote]

coté hypoténuse =
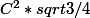
coté a =
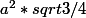
coté b =

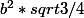
oui,
et sachant que cote c=4 et a^2 + b^2 = c^2