Exercice Fonction

[Arnaud-29-31]

Oui le réel 1 est racine évidente.

[LucieD46]

Oui le réel 1 est racine évidente.

OK mais ce que j'ai fais avant c'est possible ?

[LucieD46]

donc sa fait X(X^2 -(racine carré de 1)^2)=0
on a une équation de produit nuit :
X=0
X^2-1=0 et X=1

Possible ?

[Arnaud-29-31]

Non ... tu écris beaucoup de choses incohérentes, j'ai l'impression que tu ne maitrises pas les notions utiles ici. Il faut que tu relises le chapitre sur les trinômes en partant de la définition d'un polynôme, la notion de racine et les méthodes de factorisation.

[LucieD46]

Non ... tu écris beaucoup de choses incohérentes, j'ai l'impression que tu ne maitrises pas les notions utiles ici. Il faut que tu relises le chapitre sur les trinômes en partant de la définition d'un polynôme, la notion de racine et les méthodes de factorisation.

J'ai pas de cours. ET OUI mon prof c'est sympa.
il faut que je trouve un facteur commun ou pas ? car avec un x^3 je n'ai jamais résoud une equation.
J'avais pensé a faire le discriminant mais je n'ai pas de x^2

[Arnaud-29-31]

On ne peut pas parler de facteur commun pour un polynôme ca n'a pas de sens ici.
On doit résoudre . 1 est racine évidente donc on peut factoriser par (X-1). Ca donnera (X-1)*(qqch de degré 2).

[LucieD46]

On ne peut pas parler de facteur commun pour un polynôme ca n'a pas de sens ici.
On doit résoudre . 1 est racine évidente donc on peut factoriser par (X-1). Ca donnera (X-1)*(qqch de degré 2).

D'accord.
donc (X-1) * ( qqch de degré 2 ) = x^3 -9*x^2 + 6*x + 56
SA

[Arnaud-29-31]

Non c'est qui à 1 pour racine. Donc c'est ça que l'on factorise et non pas l'expression du début.

[LucieD46]

Non c'est qui à 1 pour racine. Donc c'est ça que l'on factorise et non pas l'expression du début.

D'accord. je vais essayer de chercher !

[LucieD46]

j'ai trouvé (X-1)*(X^2 +X -20)

[Arnaud-29-31]

Oui c'est ça. Il n'y a donc plus qu' trouver les racines du trinôme .

[LucieD46]

Oui c'est ça. Il n'y a donc plus qu' trouver les racine du trinôme .

D'accord ! Sa je sais faire ^^
Les racines sont 5 et 4 . Donc sa ces les solutions de E' et j'en déduit que ses les solutions de E puisque les deux équations sont équivalente.

[LucieD46]

Les solutions de E sont 1 ; 5 ; 4

[Arnaud-29-31]

Les solutions de E' sont X = 1 ; -5 ; 4
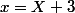
En revenant à notre changement de variable , on en déduit les solutions de E

[LucieD46]

[quote="Arnaud-29-31"]Les solutions de E' sont X = 1 ; 5 ; 4
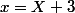
En revenant à notre changement de variable , on en déduit les solutions de E[/QUOTE


Ok pour les solution de E' mais les solutions de E sont les memes ?

[Arnaud-29-31]

Les solutions de E' c'est = 1 ; 4 ; -5
Les solution de E c'est = ...
Et et sont liées par la relation

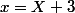
[LucieD46]

D'accord donc x= 4 ; 7 ; 8

[Arnaud-29-31]

Il y'a le signe moins qui s'était perdu devant le 5 les racines de E' c'est X = 1 ; 4 ; -5
Donc les solutions de E c'est x = 4 ; 7 et -2

[LucieD46]

Ah oui exacte !
En tout cas merci beaucoup, vous m'avez bien aidé :)

[Arnaud-29-31]

De rien. Bonne soirée.