Exercice Fonction

[Arnaud-29-31]

Non ca n'allait pas ... pour a=0 on a toujours un terme en

[LucieD46]

Non n'a n'allait pas ... pour a=0 on a toujours un terme en

et si le X^2 disparrait sa va nous donner quoi ?
Quel(s) equation faut - il utilisé ?

[Arnaud-29-31]

J'ai l'impression que tu n'as tout simplement pas compris ce que nous fait faire l'énoncé.

Tu as une équation de départ qui est l'équation (E)
On pose , ce qui correspond à changer à changer d'inconnue.

Ca nous donne qui est l'équation (E') mais qui reste équivalente à (E) puisque et sont liés. Si on résout (E') (c'est à dire si l'on trouve ) on aura résolu (E) (c'est à dire on aura trouvé )

Après développement, on trouve que (E') s'écrit
Est-ce que tu as bien trouvé ce résultat déjà ??

Ensuite l'énoncé nous dit de choisir tel que cette équation (E') s'écrive c'est à dire choisir tel qu'il n'y ait plus de terme en .

[LucieD46]

J'ai l'impression que tu n'as tout simplement pas compris ce que nous fait faire l'énoncé.

Tu as une équation de départ qui est l'équation (E)
On pose , ce qui correspond à changer à changer d'inconnue.

Ca nous donne qui est l'équation (E') mais qui reste équivalente à (E) puisque et sont liés. Si on résout (E') (c'est à dire si l'on trouve ) on aura résolu (E) (c'est à dire on aura trouvé )

Après développement, on trouve que (E') s'écrit
Est-ce que tu as bien trouvé ce résultat déjà ??

Ensuite l'énoncé nous dit de choisir tel que cette équation (E') s'écrive c'est à dire choisir tel qu'il n'y ait plus de terme en .

J'ai bien trouvé ça .
Dans ce cas faut faire = ?

[LucieD46]

Il ne sont pas trompés dans l'enoncé avec ?
Sa serai pas plutot
Vu que

[Arnaud-29-31]

Non c'est bien X^3 + pX + q car c'est l'équation (E') ... si c'était (E) que l'on voulait avoir sous cette forme il n'y aurait aucun intérêt à avoir changé de variable et introduit (E').

On a donc bien qui vérifie = . Donc = ?

[LucieD46]

Non c'est bien X^3 + pX + q car c'est l'équation (E') ... si c'était (E) que l'on voulait avoir sous cette forme il n'y aurait aucun intérêt à avoir changé de variable et introduit (E').

On a donc bien qui vérifie = . Donc = ?

Franchement aucune idée parce il y a p et q qui me dérange.
Est ce qu'il faut je le passe de l'autre côté avec

[Arnaud-29-31]

La si tu vois pas je vois mal comment t'aider plus ...

On veut a tel que X^3 + (3a-9)X^2 +(3a^2-18a+6)X + (a^3-9a^2+6a+56) = X^3 + pX +q"/> c'est à dire faire disparaitre le terme en ...

[LucieD46]

Avec les couleur j'arrive un peu mieux a comprendre:
et pour faire disparraitre le terme en X^2 normalement c'est avec une racine carré qu'il faut faire non ?

[Arnaud-29-31]

La si tu vois pas je ne vois pas comment t'aider d'avantage ...
On veut faire disparaitre le terme en pour avoir
... Comment choisir a pour faire disparaitre le terme en X^2 ? Y'a rien "a passer de l'autre coté" ou quoique ce soit la réponse est presque immédiate là.

[LucieD46]

ben quand on a un x^2 = 23
x= racine carré de 23
donc la pour faire disparaitre le X^ 2 je faire pareil avec une racine carré .
C'est possible ?

[Arnaud-29-31]

Non ... on n'a pas = quelque chose la ... ici on compare des équations.



Pour faire disparaitre le terme en , il faut que son coefficient soit nul.
Soit tout simplement est tel que

[LucieD46]

Non ... on n'a pas = quelque chose la ... ici on compare des équations.



Pour faire disparaitre le terme en , il faut que son coefficient soit nul.
Soit tout simplement est tel que

A d'accord donc forcément a =3
Question: comment je peux expliquer que le X^2 a disparu ?
Et les termes q et p sont a determiner aussi.
(3a^2-18a+6) = pX
(a^3-9a^2+6a+56) = q
C'est cohérant ou pas ?

[Arnaud-29-31]

Comment ca comment expliquer que le a disparu ? On a choisi pour que justement il disparaisse, c'est ce que demandait l'énoncé. Il n'y a rien a justifier de plus.

On avait à la base une équation du degré 3 donc avec des termes en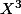 , , et un terme constant. On a changé de variable pour faire apparaitre une nouvelle équation dont les coefficients devant chaque terme dépende de et on a choisit de manière à rendre le coefficient devant nul.

Maintenant que ce est fixé, on peut donner les valeurs de et qui sont maintenant imposées. On a bien comme tu l'as écris = p et .

[LucieD46]

Comment ca comment expliquer que le a disparu ? On a choisi pour que justement il disparaisse, c'est ce que demandait l'énoncé. Il n'y a rien a justifier de plus.

On avait à la base une équation du degré 3 donc avec des termes en , , et un terme constant. On a changé de variable pour faire apparaitre une nouvelle équation dont les coefficients devant chaque terme dépende de et on a choisit de manière à rendre le coefficient devant nul.

Maintenant que ce est fixé, on peut donner les valeurs de et qui sont maintenant imposées. On a bien comme tu l'as écris = p et .

D'accord !! Enfin compris
Donc vu qu'on a=3
je remplace le par sa valeur et et je determine ainsi p et q .
donc p= -21 et q=20

[Arnaud-29-31]

Oui c'est ca.

On a donc montré qu'en posant notre équation de départ devient qui est beaucoup plus facile à résoudre que l'équation de départ.

[LucieD46]

Oui c'est ca.

On a donc montré qu'en posant notre équation de départ devient qui est beaucoup plus facile à résoudre que l'équation de départ.

d'accord mais le soucis c'est que je n'ai jamais vu pour résoudre avec X^3 ://

[Arnaud-29-31]

Tu as appris une méthode systématique pour résoudre les trinômes.
Ici on a du degré 3 mais qui présente une racine évidente. On peut donc factoriser et faire apparaître du degré 2.

[LucieD46]

a moins que sa fasse
X^3 -21X +20 = 0
X*X*X -7*3*X + 5*4 =0
X (X^2 -21 +20) = 0
X(X^2 -1X) = 0

Possibe ?

[LucieD46]

Le reel 1 est-elle la racine évidente ?