Salut,
Je veux montrer que la suite( Un); n>=2 définie par Un= sigma (k=1--->k=n) k/(n'k) est majorée
Exercice faxultatif :suites numériques
7 messages
- Page 1 sur 1
Re: Exercice faxultatif :suites numériques
IntegerX a écrit:Tu peux préciser le dénominateur de la fraction ?
Je réécris l'exercice
Montrer que la suite
Re: Exercice faxultatif :suites numériques
Salut,
Une approche possible.
0 < k/n^k <= n/n^k (puisque 1 <= k <= n)
0 < k/n^k <= 1/n^(k-1)
Un <= 1 + 1/n + 1/n² + ... 1/n^(n-1)
1 + 1/n + 1/n² + ... 1/n^(n-1) est la somme de n termes en progression géométrique de 1er terme = 1 et de raison 1/n
...

Une approche possible.
0 < k/n^k <= n/n^k (puisque 1 <= k <= n)
0 < k/n^k <= 1/n^(k-1)
Un <= 1 + 1/n + 1/n² + ... 1/n^(n-1)
1 + 1/n + 1/n² + ... 1/n^(n-1) est la somme de n termes en progression géométrique de 1er terme = 1 et de raison 1/n
...
Re: Exercice faxultatif :suites numériques
Black Jack a écrit:Salut,
Une approche possible.
0 < k/n^k <= n/n^k (puisque 1 <= k <= n)
0 < k/n^k <= 1/n^(k-1)
Un <= 1 + 1/n + 1/n² + ... 1/n^(n-1)
1 + 1/n + 1/n² + ... 1/n^(n-1) est la somme de n termes en progression géométrique de 1er terme = 1 et de raison 1/n
La raison ne peut être en fonction de n, n est variable
...
Re: Exercice faxultatif :suites numériques
Salut,
Une autre méthode :
Pour tout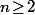 et
et 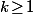 on a
on a k\!\geq\!1) ce qui toujours est vrai donc le plus grand terme de la somme
ce qui toujours est vrai donc le plus grand terme de la somme 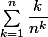 c'est le premier
c'est le premier 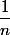 et, comme il y a
et, comme il y a  termes, c'est que leur somme
termes, c'est que leur somme 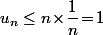 .
.
On peut même faire mieux en disant qu'à part le premier terme, ils sont tous inférieur au deuxième terme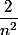 donc
donc 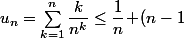\!\times\!\dfrac{2}{n^2}\leq\dfrac{3}{n}) .
.
Une autre méthode :
Pour tout
On peut même faire mieux en disant qu'à part le premier terme, ils sont tous inférieur au deuxième terme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 77 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
