Exercice dont je ne comprends pas l'énoncé.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonyme
 par Anonyme » 20 Jan 2011, 19:26
par Anonyme » 20 Jan 2011, 19:26
Hellow,
On me dit,
"On considère dans un repère, l'hyperbole HL d'équation y = 1/x et les trois points A(1;-1), B(1;2) et C(2;0)"
1_ Tracez l'hyperbole HL et placez les points A, B, C.
Combien semble t-il y avoir de tangentes à HL passant par A ? Par B ? Par C ?
2_M(x;y) est un point du plan. Pour a =/=0, P désigne le point de HL d'abscisse a, DELTA est la tangente à HL au point P. Dire "M appartient à DELTA" équivaut à dire "a²y-2a+x = 0"
Pourquoi ?
La 1_, c'est OK, mais la 2 j'ai pas mals de difficultés :(
Je n'arive pas à savoir ce que a²y-2a+x=0 correspond ..
Je pebsais à l'équation de la tangente en P, mais ça n'a pas l'air d'être ça ..
M et P ont le même coeeficient directeur, mais j'arrive pas à creuser ça :(
Merci de m'éclaircir :)
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 20 Jan 2011, 20:07
par XENSECP » 20 Jan 2011, 20:07
Si tu connais pas les formules c'est sûr que c'est pas évident....
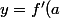 (x-a) + f(a))
l'équation de la tangente au point d'abscisse a
-
Anonyme
 par Anonyme » 20 Jan 2011, 20:09
par Anonyme » 20 Jan 2011, 20:09
Oui,
Je les connais ..
Mais je ne vois pas à quoi elle correspond, je ne la comprends pas (Celle de l'exo) :(
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 20 Jan 2011, 20:11
par XENSECP » 20 Jan 2011, 20:11
Euh et si j'écris
 = \dfrac 1x)
ça s'éclaire ?
-
Anonyme
 par Anonyme » 20 Jan 2011, 20:15
par Anonyme » 20 Jan 2011, 20:15
Yep,
J'ai déjà tenter de developper à partir de y = f(x) + f'(a)(x-a), mais je bloque 0o
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 20 Jan 2011, 20:17
par XENSECP » 20 Jan 2011, 20:17
Développes ici pour voir -.-
-
Anonyme
 par Anonyme » 20 Jan 2011, 20:23
par Anonyme » 20 Jan 2011, 20:23
^^
y=f(a)+f'(a)(x-a)
=1/a + 1/a² (X-a)
=1/a + 1/a²X - 1/a²a
=a²/a(a²) + a/a(a²)X - a/a(a²)a
=(a²+ax-a²)/a(a²)
=ax/a(a²)
=x/a²
...
Désolé pour la forme :(
-
bmiras
- Membre Naturel
- Messages: 67
- Enregistré le: 18 Jan 2011, 00:51
-
 par bmiras » 20 Jan 2011, 22:09
par bmiras » 20 Jan 2011, 22:09
2vieux' a écrit:^^
y=f(a)+f'(a)(x-a)
=1/a + 1/a² (X-a)
=1/a + 1/a²X - 1/a²a
=a²/a(a²) + a/a(a²)X - a/a(a²)a
=(a²+ax-a²)/a(a²)
=ax/a(a²)
=x/a²
...
Désolé pour la forme

Ca ne marche pas vraiment bien ton truc...
Déjà combien vaut f'(x) pour f(x)=1/X ?
-
XENSECP
- Habitué(e)
- Messages: 6387
- Enregistré le: 27 Fév 2008, 19:13
-
 par XENSECP » 20 Jan 2011, 22:12
par XENSECP » 20 Jan 2011, 22:12
bmiras a écrit:Ca ne marche pas vraiment bien ton truc...
Déjà combien vaut f'(x) pour f(x)=1/X ?
C'est ça... Avec la vraie dérivée c'est mieux !
-
Anonyme
 par Anonyme » 21 Jan 2011, 19:19
par Anonyme » 21 Jan 2011, 19:19
f'(x) pour f(x) = 1/x = -1/x² ..
C'est là que me suis planté alors ^^ Une erreur de signe :X
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 57 invités
