Exercice dérivée term S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 15:57
par sophie77 » 07 Nov 2012, 15:57
Bonjour tout le monde,
Je bloque sur un exercice qui est tout simple je pense...
On considère la fonction f définie sur R par :
F(x) = 2sin ( x/2 + pi/3 ).
Déterminer les abscisses des points en lesquels la fonction dérivée de f s'annule.
Donc une fois que j'ai calculé la dérivée , je ne sais pas quoi faire. Pour la dérivée je trouve cos 2pi/3
Merci de m'éclairer !!!
-
sylvain.s
- Membre Rationnel
- Messages: 679
- Enregistré le: 18 Oct 2012, 15:52
-
 par sylvain.s » 07 Nov 2012, 16:08
par sylvain.s » 07 Nov 2012, 16:08
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Nov 2012, 16:24
par Arnaud-29-31 » 07 Nov 2012, 16:24
Bonjour,
Comment t'y prends tu pour trouver la dérivée ?
Ici on reconnait sin(u) dans l'expression de F(x), avec u fonction de x.
Quelle est la dérivée de sin(u) ?
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 16:29
par sophie77 » 07 Nov 2012, 16:29
Bonjour, merci de ton aide
Tu as certainement raison mais j'ai refait les calculs e je ne comprends pas comment tu arrives à ce résultat...
En fait j'ai utilisé la formule de la dérivée de x --> f (ax+b)
Donc f'(x) = a * f'(ax+b) avec ici a = 0.5 et f'(ax+b)= 2cos ( (3x + 2pi) / 6 ) c'est bon je trouve comme toi, j'ai compris mon erreur ! Par contre je ne comprends pas pourquoi tu met + 0.5 ...car dans la formule on multiplie par a et donc ici par 0.5....
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Nov 2012, 16:34
par Arnaud-29-31 » 07 Nov 2012, 16:34
Attention aux notations, tu écris deux fonctions avec la même lettre alors que ce ne sont pas les même ... a part ça c'est bien l'idée : la dérivé de
)
c'est bien
)
.
Donc si on reprend le calcul avec notre fonction, ca donne quoi ?
-
sylvain.s
- Membre Rationnel
- Messages: 679
- Enregistré le: 18 Oct 2012, 15:52
-
 par sylvain.s » 07 Nov 2012, 16:41
par sylvain.s » 07 Nov 2012, 16:41
Je suis désolé j'ai fait une erreur de formule,
au lieu dérivée f(ax+b)=a*f'(ax+b) j'ai additionné ^^; tu avais raison, par contre tu as oublié quelque chose dans cos 2pi/3
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 16:59
par sophie77 » 07 Nov 2012, 16:59
Ah d'accord...
Donc si je reprends ça donne : f'(x) = cos 2pi/3 + x ??
parce qu'avant je trouvais que cos 2pi/3 et j'avais pas de x donc je comprenais pas comment faire...mais là avec un x on peut trouver les abscisses non ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Nov 2012, 17:05
par Arnaud-29-31 » 07 Nov 2012, 17:05
Non ...
Ta propriété sur la dérivée de f(ax+b) appliquée au sin ca donne
]' = a \times cos(ax+b))
la dérivée du sinus étant le cosinus.
Donc la dérivée de ta fonction F qu'est ce que ca donne ?
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 07 Nov 2012, 17:14
par annick » 07 Nov 2012, 17:14
Bonjour,
ça me paraît bien compliqué ta formule.
Normalement tu as aussi dû apprendre
(sinu)'=u' cosu
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 17:24
par sophie77 » 07 Nov 2012, 17:24
Arnaud-29-31 a écrit:Non ...
Ta propriété sur la dérivée de f(ax+b) appliquée au sin ca donne
]' = a \times cos(ax+b))
la dérivée du sinus étant le cosinus.
Donc la dérivée de ta fonction F qu'est ce que ca donne ?
Eh bien en appliquant ta formule je retombe toujours sur la même chose..Je ne comprends pas...
-
sylvain.s
- Membre Rationnel
- Messages: 679
- Enregistré le: 18 Oct 2012, 15:52
-
 par sylvain.s » 07 Nov 2012, 17:25
par sylvain.s » 07 Nov 2012, 17:25
f'(x) = cos(0.5x + pi/3)
C'est le 0.5x que tu zappes
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Nov 2012, 17:27
par Arnaud-29-31 » 07 Nov 2012, 17:27
Ce qu'il y a sous le sin ou cos ne doit pas bouger, on ne fait que sortir un coeff
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 17:34
par sophie77 » 07 Nov 2012, 17:34
Arnaud-29-31 a écrit:Ce qu'il y a sous le sin ou cos ne doit pas bouger, on ne fait que sortir un coeff
donc c'est pas correct d'écrire f'(x)= cos (0.5x + pi/3) ??
-
sylvain.s
- Membre Rationnel
- Messages: 679
- Enregistré le: 18 Oct 2012, 15:52
-
 par sylvain.s » 07 Nov 2012, 17:41
par sylvain.s » 07 Nov 2012, 17:41
sophie77 a écrit:donc c'est pas correct d'écrire f'(x)= cos (0.5x + pi/3) ??
si c'est juste, tu avais changé ce qu'il y avait sous le sin
on avait 2sin(0.5x+ pi/3)
Et toi quand tu as dérivé, tu as changé (0.5x+ pi/3) en (2 pi/3)
tu as marqué cos (2 pi/3), en plus tu as même pas de "x" dans ta dérivée.
alors que c'est bien cos(0.5x + pi/3)
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 17:47
par sophie77 » 07 Nov 2012, 17:47
Ahhhhhh c'est bon j'ai compris !!! merci pour ton explication :)
Je vais finir l'exo et je reviendrai vers vous pour vous demander si c'est juste...
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 20:33
par sophie77 » 07 Nov 2012, 20:33
Alors maintenant que j'ai f'(x)=cos (x/2 + pi/3) , je peux dire que cos pi/3 = 1/2
Donc ça fait Cos (2pi/3)
C'est correct de dire ça ?
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 07 Nov 2012, 20:35
par sophie77 » 07 Nov 2012, 20:35
Ah j'ai oublié le x...mince
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 07 Nov 2012, 20:44
par Arnaud-29-31 » 07 Nov 2012, 20:44
On a bien
 = cos ( \frac{x}{2} + \frac{\pi}{3} ))
pour le reste je comprends pas bien ce que tu racontes ... On doit trouver les valeurs de

pour lesquelles
 = 0)
-
sophie77
- Membre Naturel
- Messages: 15
- Enregistré le: 29 Déc 2011, 21:56
-
 par sophie77 » 08 Nov 2012, 12:40
par sophie77 » 08 Nov 2012, 12:40
Donc on a f'(x)= (cosx) /2 + cos pi/3
donc comme tu dis, on doit trouver les valeurs de x pour lesquelles f'(x)=0
eh bien là faut faire comment ?? Faut bien dire que cos 1/2 = pi/3 pour arriver à simplifier tout ça non ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 08 Nov 2012, 15:06
par Arnaud-29-31 » 08 Nov 2012, 15:06
Non
)
ce n'est pas ça ...
)
c'est
)
Je ne vois pas ce que ca t'apporte de dire que
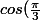 = \frac12)
...
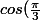)
n'apparait nulle part.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
