Bonjour à tous ! J'aurrai besoin d'aide pour un exercice
Dans un remère orthonormé, p est la parabole d'équation y=x^2 et A est le point de coordonnées (1;-2).
Samantha conjecture qu'il existe deux tangeante à P passant par A.
On se propose de démontrer cette conjecture.
J'ai fait les deux première question et celle qui bloque c'est celle là
c) Déterminer les équations des deux tangentes à P qui passent par A.
Si vous pouviez m'aider...
Exercice dérivation
6 messages
- Page 1 sur 1
Re: Exercice dérivation
Quelle est l'équation réduite d'une droite passant par le point A ?
(Si tu appelles m son coefficient angulaire, elle s'exprime en fonction de m)
Cette droite sera tangente à la parabole si et seulement si elle la coupe en 2 points confondus ...
(Si tu appelles m son coefficient angulaire, elle s'exprime en fonction de m)
Cette droite sera tangente à la parabole si et seulement si elle la coupe en 2 points confondus ...
Re: Exercice dérivation
Le titre "exercice dérivation " impose cette deuxième méthode :
La tangente en) a pour équation réduite :
a pour équation réduite : 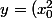'.(x -x_0)+x_0^2=2x.x_0-x_0^2)
On écrit qu'elle passe par le point A(1; -2) et on obtient l'équation du second degré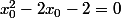 dont les solutions sont les abscisses des 2 points de tangence.
dont les solutions sont les abscisses des 2 points de tangence.
La tangente en
On écrit qu'elle passe par le point A(1; -2) et on obtient l'équation du second degré
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 100 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
