Bonjour,
J'ai un exercice de maths à faire et je n'arrive pas à répondre à une question (et du coup je peux pas faire la suite...) Voici l'énoncé :
Soit ABCD un carré et M un point de la diagonale [AC].
Soit P le pid de la perpendiculaire issue de M sur la droite (AD) et Q celui de la perpendiculaire issue de M sur la droite (CD).
On considère le repère orthonormé (A ; B ; D)
1. Si on note x l'abscisse du point M, quelle est son ordonnée ?
2. A quel intervalle x doit-il appartenir ?
3a. Déterminer en fonction de x les coordonnées des points P et Q.
3b. En déduire que, quelle que soit la position du point M, on a MB = PQ
3c. Donner une démonstration géométrique de ce résultat.
4. Soit E le point tel que MQPE soit un parallélogramme.
4a. Déterminer les coordonnées du points E en fonction de x.
4b. Quelle est la nature du triangle BME ?
4c. En déduire que les droites (MB) et (PQ) sont perpendiculaires.
---
Pour commencer j'ai fais un repère en prenant AB comme abcisse et AD comme ordonnée puis j'ai fais le carré ABCD et j'ai placé le point M sur la diagonale [AC]. Ensuite j'ai placé P sur [AD] et Q sur [DC](de façon à ce qu'ils soient les pieds des perpendiculaires)
Donc j'ai répondu à la question 1, 2 et 3a mais la 4a je n'y arrive pas et sans celle ci je ne peux pas répondre à la 4b et 4c...
1. Si l'abcisse du point M est égal à x, son ordonnée est elle aussi égale à x
2. x appartient à [0;1]
3a. P(0;x) et Q(x;1)
Merci d'avance :)
Exercice : bases de la géométrie plane
12 messages
- Page 1 sur 1
laurie87 a écrit:Bonjour,
J'ai un exercice de maths à faire et je n'arrive pas à répondre à une question (et du coup je peux pas faire la suite...) Voici l'énoncé :
Soit ABCD un carré et M un point de la diagonale [AC].
Soit P le pid de la perpendiculaire issue de M sur la droite (AD) et Q celui de la perpendiculaire issue de M sur la droite (CD).
On considère le repère orthonormé (A ; B ; D)
1. Si on note x l'abscisse du point M, quelle est son ordonnée ?
2. A quel intervalle x doit-il appartenir ?
3a. Déterminer en fonction de x les coordonnées des points P et Q.
3b. En déduire que, quelle que soit la position du point M, on a MB = PQ
3c. Donner une démonstration géométrique de ce résultat.
4. Soit E le point tel que MQPE soit un parallélogramme.
4a. Déterminer les coordonnées du points E en fonction de x.
4b. Quelle est la nature du triangle BME ?
4c. En déduire que les droites (MB) et (PQ) sont perpendiculaires.
---
Pour commencer j'ai fais un repère en prenant AB comme abcisse et AD comme ordonnée puis j'ai fais le carré ABCD et j'ai placé le point M sur la diagonale [AC]. Ensuite j'ai placé P sur [AD] et Q sur [DC](de façon à ce qu'ils soient les pieds des perpendiculaires)
Donc j'ai répondu à la question 1, 2 et 3a mais la 4a je n'y arrive pas et sans celle ci je ne peux pas répondre à la 4b et 4c...
1. Si l'abcisse du point M est égal à x, son ordonnée est elle aussi égale à x
2. x appartient à [0;1]
3a. P(0;x) et Q(x;1)
Merci d'avance
Q est sur la droite (DC) parallèle à l'axe AB et M se trouve sur la perpendiculaire passant par Q, donc quel sera son ordonnée ?
Bonjour,
il y a , me semble-t-il des erreurs dans l'enoncé!
si MQPE est un parallelogramme on doit avoir PE parallele a MQ et |PE|=|MQ|
donc E est sur AD et AE = AD+DE = 2x
les triangles MPA et MPE sont rectangles en P et isoceles donc |MP|=|PA|=|AE|
par suite le triangle AME est rectangle ET NON le triangle BME!!!!
.....
il y a , me semble-t-il des erreurs dans l'enoncé!
si MQPE est un parallelogramme on doit avoir PE parallele a MQ et |PE|=|MQ|
donc E est sur AD et AE = AD+DE = 2x
les triangles MPA et MPE sont rectangles en P et isoceles donc |MP|=|PA|=|AE|
par suite le triangle AME est rectangle ET NON le triangle BME!!!!
.....
siger a écrit:Bonjour,
il y a , me semble-t-il des erreurs dans l'enoncé!
si MQPE est un parallelogramme on doit avoir PE parallele a MQ et |PE|=|MQ|
donc E est sur AD et AE = AD+DE = 2x
les triangles MPA et MPE sont rectangles en P et isoceles donc |MP|=|PA|=|AE|
par suite le triangle AME est rectangle ET NON le triangle BME!!!!
.....
E sera plutôt sur [CD] puisque Q est sur [CD]
siger a écrit:Bonjour,
il y a , me semble-t-il des erreurs dans l'enoncé!
si MQPE est un parallelogramme on doit avoir PE parallele a MQ et |PE|=|MQ|
donc E est sur AD et AE = AD+DE = 2x
les triangles MPA et MPE sont rectangles en P et isoceles donc |MP|=|PA|=|AE|
par suite le triangle AME est rectangle ET NON le triangle BME!!!!
.....
Bonsoir,
Il n'y a pas d'erreurs puisque c'est un exercice qui vient du livre (et les erreurs sont rares) mais si vous voulez je peux vous donner un shéma du dessin qu'un camarade m'a envoyé !
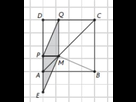
voilà je pense l'avoir insérer, la voyez-vous ?
merci !
re
oui merci
autant pour moi, j'ai mal lu (et relu) l'enonce et j'ai place P sur AB!
MQPE etant un parallelogramme on a :
MQ parallele a PE donc E est sur Oy
|MQ|=|PE|= |DP| donc P est le milieu de DE
d'ou yE = AE= ....
par construction les triangles DPM et EPM sont egaux ( rectangle avec deux cotes egaux) et par suite les angles (PDM) et (PEM) sont egaux
soit Q´ l'intersection de QM avec AB
les triangles DPM et BQ´M sont egaux ainsi que (PDM) et (MBQ´)
finalement les angles (PEM) et (ABM) sont egaux
les droites BM et EM faisant des angles egaux avec deux droites perpendiculaires AB et AE sont elles -meme perpendiculaires
complement: pour la 3b il faut utiliser les coordonnees des points et calculer les segments
pour la 3 c il faut utiliser les proprietes de symetrie du carre par rapport a une diagonale
oui merci
autant pour moi, j'ai mal lu (et relu) l'enonce et j'ai place P sur AB!
MQPE etant un parallelogramme on a :
MQ parallele a PE donc E est sur Oy
|MQ|=|PE|= |DP| donc P est le milieu de DE
d'ou yE = AE= ....
par construction les triangles DPM et EPM sont egaux ( rectangle avec deux cotes egaux) et par suite les angles (PDM) et (PEM) sont egaux
soit Q´ l'intersection de QM avec AB
les triangles DPM et BQ´M sont egaux ainsi que (PDM) et (MBQ´)
finalement les angles (PEM) et (ABM) sont egaux
les droites BM et EM faisant des angles egaux avec deux droites perpendiculaires AB et AE sont elles -meme perpendiculaires
complement: pour la 3b il faut utiliser les coordonnees des points et calculer les segments
pour la 3 c il faut utiliser les proprietes de symetrie du carre par rapport a une diagonale
siger a écrit:re
oui merci
autant pour moi, j'ai mal lu (et relu) l'enonce et j'ai place P sur AB!
MQPE etant un parallelogramme on a :
MQ parallele a PE donc E est sur Oy
|MQ|=|PE|= |DP| donc P est le milieu de DE
d'ou yE = AE= ....
par construction les triangles DPM et EPM sont egaux ( rectangle avec deux cotes egaux) et par suite les angles (PDM) et (PEM) sont egaux
soit Q´ l'intersection de QM avec AB
les triangles DPM et BQ´M sont egaux ainsi que (PDM) et (MBQ´)
finalement les angles (PEM) et (ABM) sont egaux
les droites BM et EM faisant des angles egaux avec deux droites perpendiculaires AB et AE sont elles -meme perpendiculaires
complement: pour la 3b il faut utiliser les coordonnees des points et calculer les segments
pour la 3 c il faut utiliser les proprietes de symetrie du carre par rapport a une diagonale
Merci pour votre réponse complète et détaillée..
Cependant, que dois-je faire avec tout cela ? Mais surtout, avec tout cela que dois-je faire pour trouver l'ordonnée de E ?
Excusez moi j'ai un peu de mal avec les maths
Merci à vous et bonne soirée
tu sais que P est le milieu de DE et que E est sur Ox
par suite tu sais que
xE = 0. ( E sur Oy)
et que yP =( yE + yD)/2 (P est le milieu de DE)
d'ou
yE = 2yP - yD
....
pour demontrer que les droites sont perpendiculaires il y a plus simple que ce que j'ai ecrit
les triangles DPM et EMP sont egaux ( rectangles,un cote commun et deux cotes egaux )
les triangles DMA et BMA sont egaux ( un angle egal : pi/4, un cote commun, deux cotes egaux),
donc les angles (AEM) et (ABM) sont egaux
...deux droites faisant des angles egaux ....
par suite tu sais que
xE = 0. ( E sur Oy)
et que yP =( yE + yD)/2 (P est le milieu de DE)
d'ou
yE = 2yP - yD
....
pour demontrer que les droites sont perpendiculaires il y a plus simple que ce que j'ai ecrit
les triangles DPM et EMP sont egaux ( rectangles,un cote commun et deux cotes egaux )
les triangles DMA et BMA sont egaux ( un angle egal : pi/4, un cote commun, deux cotes egaux),
donc les angles (AEM) et (ABM) sont egaux
...deux droites faisant des angles egaux ....
siger a écrit:tu sais que P est le milieu de DE et que E est sur Ox
par suite tu sais que
xE = 0. ( E sur Oy)
et que yP =( yE + yD)/2 (P est le milieu de DE)
d'ou
yE = 2yP - yD
....
yE = 2yP- yD
= 2x - 1
est-ce cela ?
si oui, les coordoonées de E sont (0;2x-1) ?
Merci encore de consacrer votre temps pour moi !
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 60 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
