Exercice avec des résistances

par **Ziina95** » 31 Oct 2011, 22:40

Bonjour,
J'ai un DM de maths avec 1 exercice qui porte sur les résistances. Voici l'exercice : On dispose de deux résistances électriques R1 et R2. Lors d'un montage en série, on obtient une résistance équivalante de 135;) et lors d'un montage en parallèle, on obtient une résistance équivalente de 30;). Déterminer les valeurs R1 et R2.
Comment dois-je faire ?? Aidez moi svp..

--------------------------------------------------------------------------------
Mzelle Ziina

par **gcgp** » 31 Oct 2011, 22:50

la résistance équivalente lors d'un montage en série équivaut à la somme de tes résistances

la résistance équivalente lors d'un montage en parallèle équivaut à la somme des inverses de tes résistances

Tu as donc deux équations, deux inconnues

par **Adoration_For_None** » 31 Oct 2011, 22:52

Bonsoir,

Si mes souvenirs de MPI sont bons :

Soit n résistances Ri montées en série et R la résistance équivalente résultant de ce montage. Alors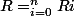

.

Soit n résistances Ri montées en parallèle et R' la résistance équivalente résultant de ce montage. Alors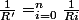

.

Ainsi dans ton cas tu peux poser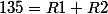

et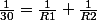

.
On doit alors résoudre le système d'équations suivant :

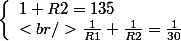
Bon courage !

par **Adoration_For_None** » 31 Oct 2011, 22:54

gcgp a écrit:la résistance équivalente lors d'un montage en série équivaut à la somme de tes résistances

la résistance équivalente lors d'un montage en parallèle équivaut à la somme des inverses de tes résistances

Tu as donc deux équations, deux inconnues

Non, c'est l'inverse de la résistance équivalente qui équivaut à la somme des inverses des résistances associées en parallèle.

par **gcgp** » 31 Oct 2011, 22:56

Autant pour moi, jai omis "inverse" ^^

par **Adoration_For_None** » 31 Oct 2011, 23:08

En tout cas, avec la mise au même dénominateur ça sent le second degré à plein nez !
Il va falloir faire attention à quel racine du polynôme choisir, il y en a aura une qui marchera, l'autre non.
Pour t'aider 0
Puis même... On peut pas dire R1 égal tant ... et R2 égal tant ...
Mais seulement si R1 vaut tant, alors R2 vaut tant et inversement.
Parce qu'on ne sait pas qui de R1 ou R2 est la quantité la plus grande.

Exercice avec des résistances

Exercice avec des résistances

Qui est en ligne