Exercice arithmétique FIN TS
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 31 Aoû 2010, 18:17
par Dinozzo13 » 31 Aoû 2010, 18:17
Salut à tous !!!
Djmaxgamer et moi callons sur l'exercice d'arithmétique suivant :
Montrer que quel que soit l'entier naturel

, le quotient

est irréductible.
Je pense qu'il faudrait partir du fait de nommer soit p un nombre premier diviseur commun du numérateur et du dénominateur mais après, il doit y avoir une astuce toute conne mais on la trouve pas :triste:
Merci d'avance pour l'aide apportée :++:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 18:34
par benekire2 » 31 Aoû 2010, 18:34
Salut cela revient a montrer que
=1)
Tu peut remarquer que
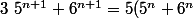+6^n)
ainsi
=pgcd(5^n+6^n,6^n)=pgcd(5^n,6^n))
Tu peut conclure ,
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 31 Aoû 2010, 18:35
par Dinozzo13 » 31 Aoû 2010, 18:35
benekire2 a écrit:Salut cela revient a montrer que
=1)
Tu peut remarquer que
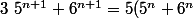+6^n)
ainsi
=pgcd(5^n+6^n,6^n)=pgcd(5^n,6^n))
Tu peut conclure ,
Pas besoin du nombre premier p alors ?
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 31 Aoû 2010, 18:36
par Dinozzo13 » 31 Aoû 2010, 18:36
benekire2 a écrit:Tu peut remarquer que
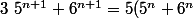+6^n)
Voilà l'astuce toute conne qu'on attendais meric :++:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 18:36
par benekire2 » 31 Aoû 2010, 18:36
non je ne pense pas !
PS. J'ai posté le bac marocain pour toi !!
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 31 Aoû 2010, 18:38
par Dinozzo13 » 31 Aoû 2010, 18:38
benekire2 a écrit:P.S. : j'ai posté le bac marocain pour toi !
Ah désolé, j'ai pas trop eu le temps d'aller sur Maths Forum aujourd'hui j'irai voir alors, merci :++:
-
benekire2
- Membre Transcendant
- Messages: 4678
- Enregistré le: 08 Avr 2009, 16:39
-
 par benekire2 » 31 Aoû 2010, 18:40
par benekire2 » 31 Aoû 2010, 18:40
Le plus simple pour conclure c'est la décomposition en facteurs premiers, tu montre que pgcd(a,b)=1 => pgcd(a^n,b^n)=1
or 5 et 6 sont premiers entre eux ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
