Exercice 1ere
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 20:47
par Laura19 » 13 Nov 2013, 20:47
Bonjour, je dois représenter f:x --> x²-2x-1
et je ne sais pas du tout comment m'y prendre.
Pouvez-vous m'aider svp...
Merci d'avance
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 20:54
par Fred_Sabonnères » 13 Nov 2013, 20:54
Bonsoir
Déterminer le domaine de définition de f
Calculer la fonction dérivée f'
Déterminer la ou les valeurs pour lesquelles f'(x)=0
Déterminer la ou les valeurs pour lesquelles f(x)=0
Déterminer les limites
Faire le tableau de variation
Puis tracer la fonction
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 20:55
par Laura19 » 13 Nov 2013, 20:55
Et comment je fais tout ça ??
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 20:57
par Fred_Sabonnères » 13 Nov 2013, 20:57
On va commencer par le domaine de définition.
Quel est l'ensemble de définition de cette fonction?
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 13 Nov 2013, 20:59
par Frednight » 13 Nov 2013, 20:59
la forme du trinôme te rappelle vaguement quelle identité remarquable?
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:01
par Laura19 » 13 Nov 2013, 21:01
Fred_Sabonnères a écrit:On va commencer par le domaine de définition.
Quel est l'ensemble de définition de cette fonction?
Je ne sais pas :/
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:02
par Laura19 » 13 Nov 2013, 21:02
Frednight a écrit:la forme du trinôme te rappelle vaguement quelle identité remarquable?
la première : (a-b)²
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 21:04
par Fred_Sabonnères » 13 Nov 2013, 21:04
Tu es en première quelle section?
As-tu entendu parlé de discriminant? de polynôme du second degrés?
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:08
par Laura19 » 13 Nov 2013, 21:08
Oui mais je ne sais pas comment on calcule l'ensemble de définition...
-
Frednight
- Membre Rationnel
- Messages: 616
- Enregistré le: 04 Fév 2007, 17:03
-
 par Frednight » 13 Nov 2013, 21:15
par Frednight » 13 Nov 2013, 21:15
Laura19 a écrit:la première : (a-b)²
effectivement :
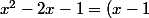^2-2)
concernant
^2)
, on peut dire que ça ressemble assez à

non? Si le minimum de
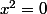
est atteint pour

, qu'en est-il pour
^2)
?
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 21:15
par Fred_Sabonnères » 13 Nov 2013, 21:15
J'ai été jeter un coup dil à ton programme. Pour faire le tableau de variation, il faut d'abord trouver les valeurs pour lesquelles f(x)=0.
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:17
par Laura19 » 13 Nov 2013, 21:17
Je calcule le discriminant ?
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 21:22
par Fred_Sabonnères » 13 Nov 2013, 21:22
Oui. Tu en déduis les racines du trinôme.
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:26
par Laura19 » 13 Nov 2013, 21:26
= 2²-4 X (-1)
= 8
x1= (2-racine carré de 8) / 2
x1= -0,8
x2= (2+ racine carré de 8) / 2
x2= 2,4
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 21:30
par Fred_Sabonnères » 13 Nov 2013, 21:30
Ca peut se simplifier en

mais c'est ça :ptdr:
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:33
par Laura19 » 13 Nov 2013, 21:33
Ok :) Et donc après je fais quoi ?
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 21:42
par Fred_Sabonnères » 13 Nov 2013, 21:42
On a donc 2 racines distinctes. Tu en déduis que le signe de f à l'extérieur des racines est positif (du signe du coef devant x²).
La représentation graphique d'une fonction trinôme définie par f(x) =ax2+bx+c est une parabole.
Son sommet a pour abscisse -b/2a et pour ordonnée f(-b/2a).
-
Fred_Sabonnères
- Membre Relatif
- Messages: 221
- Enregistré le: 07 Oct 2007, 16:04
-
 par Fred_Sabonnères » 13 Nov 2013, 21:56
par Fred_Sabonnères » 13 Nov 2013, 21:56
Tu dois obtenir quelque chose comme ça :zen:
 &\nearrow&0&\nearrow &+\infty\end{array})
-
Laura19
- Membre Naturel
- Messages: 87
- Enregistré le: 09 Nov 2012, 19:18
-
 par Laura19 » 13 Nov 2013, 21:57
par Laura19 » 13 Nov 2013, 21:57
Son sommet c'est -2/2 ? Donc -1 ??
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
