Etudier le signe d'une dérivée
14 messages
- Page 1 sur 1
Etudier le signe d'une dérivée
Bonjour, je dois étudier le signe de f'(x) pour ensuite établir le tableau de variation de f mais je ne sais pas comment faire :
J'ai dérivé f(x) et j'ai trouvé f'(x)= 1/(x+1)²
Mais après ça je ne sais pas du tout quoi faire...
Merci d'avance
J'ai dérivé f(x) et j'ai trouvé f'(x)= 1/(x+1)²
Mais après ça je ne sais pas du tout quoi faire...
Merci d'avance
Re
ne confonds pas tout!
f(x) = -1/(x+1) pour que la derivée soit celle que tu indiques
f'(x) = 1/(x+1)² est toujours positive (il n'y a rien a etudier dans ce cas)
donc
f(x) est toujours croissante
mais f(x) n'est pas definie pour x=-1
la fonction croit donc de 0 a +infini pour x<-1
et de -infini a 0 pour x>-1
ne confonds pas tout!
f(x) = -1/(x+1) pour que la derivée soit celle que tu indiques
f'(x) = 1/(x+1)² est toujours positive (il n'y a rien a etudier dans ce cas)
donc
f(x) est toujours croissante
mais f(x) n'est pas definie pour x=-1
la fonction croit donc de 0 a +infini pour x<-1
et de -infini a 0 pour x>-1
Pour compléter, l'important de ce rappeler est que :
Si la dérivée de f, f'(x) est positif quel que soit x alors la fonction f est croissante.
D'autres cas existent, un exemple
Si f'(x) est positif sur l'intervalle ]-infini, 0] (quel que soit x entre -infini et 0)
et f'(x) est négatif sur l'intervalle ]0, +infini[
alors la fonction f est croissante puis décroissante avec le changement en 0.
C'est pour ça que lorsqu'on veut étudier les variations de f on résout f'(x) = 0, il y a autant de changement de monotonie (croissante/décroissante) que de solutions à cette équation.
Si la dérivée de f, f'(x) est positif quel que soit x alors la fonction f est croissante.
D'autres cas existent, un exemple
Si f'(x) est positif sur l'intervalle ]-infini, 0] (quel que soit x entre -infini et 0)
et f'(x) est négatif sur l'intervalle ]0, +infini[
alors la fonction f est croissante puis décroissante avec le changement en 0.
C'est pour ça que lorsqu'on veut étudier les variations de f on résout f'(x) = 0, il y a autant de changement de monotonie (croissante/décroissante) que de solutions à cette équation.
Non que f'(x) est positif quel que soit x donc f est croissante.
Il ne faut rien changer de cette phrase. f'(x) n'est pas croissant, pour le savoir il faudrait calculer f''(x).
Pas besoin de tableau de signes ici, on fait un tableau quand f'(x) peut être positif ou négatif selon la valeur de x. Pour dire dans quels intervalles de x elle (f'(x)) est positif ou négatif.
Il ne faut rien changer de cette phrase. f'(x) n'est pas croissant, pour le savoir il faudrait calculer f''(x).
Pas besoin de tableau de signes ici, on fait un tableau quand f'(x) peut être positif ou négatif selon la valeur de x. Pour dire dans quels intervalles de x elle (f'(x)) est positif ou négatif.
Re,
Si elle l'est. Quel que soit x, il existe un x' plus grand tel que f(x') > f(x) sur chaque partie continue de la fonction.
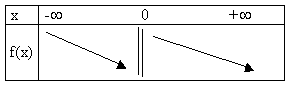
Pour que ce soit plus clair, on pourrait tout de même faire un tableau ici. Avec une double barre quand x = -1 et deux "+" pour f' et deux flèches qui montent pour f de chaque côté de la double barre.
Si elle l'est. Quel que soit x, il existe un x' plus grand tel que f(x') > f(x) sur chaque partie continue de la fonction.
Pour que ce soit plus clair, on pourrait tout de même faire un tableau ici. Avec une double barre quand x = -1 et deux "+" pour f' et deux flèches qui montent pour f de chaque côté de la double barre.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :