Etude de variation et de signe fonction exponentielle
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 11 Mai 2015, 15:22
par novicemaths » 11 Mai 2015, 15:22
Bonjour
Voici une fonction
=\frac{e^-^x}{1-x})
c'est une fonction de forme
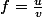
avec
=e^-^x)
et
=1-x)
D'où
=-e^-^x)
et
=-1)
Donc,
=\frac{u'v-uv'}{v^2})
soit
=\frac{(-e^-^x)(1-x)-(e^-^x)(-1)}{(1-x)^2})
=
}{(1-x)^2})
=
^2})
J'ignore si mon calcul est juste.
Si il est juste, à partir de là je ne vois pas comment étudier la variation de f l'étude de signe.
Pourriez-vous m'indiquer la démarche?
A +
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 11 Mai 2015, 16:25
par Manny06 » 11 Mai 2015, 16:25
novicemaths a écrit:Bonjour
Voici une fonction
=\frac{e^-^x}{1-x})
c'est une fonction de forme
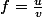
avec
=e^-^x)
et
=1-x)
D'où
=-e^-^x)
et
=-1)
Donc,
=\frac{u'v-uv'}{v^2})
soit
=\frac{(-e^-^x)(1-x)-(e^-^x)(-1)}{(1-x)^2})
=
}{(1-x)^2})
=
^2})
J'ignore si mon calcul est juste.
Si il est juste, à partir de là je ne vois pas comment étudier la variation de f l'étude de signe.
Pourriez-vous m'indiquer la démarche?
A +
Ta dérivée est correcte
elle a le signe de x
tu peux donc faire le tableau de varaition
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 12 Mai 2015, 06:14
par novicemaths » 12 Mai 2015, 06:14
Bonjour
Le problème est que je ne vois pas comment faire le tableau variation, j'ai oublié de vous dire que f est définie sur

.
A +
-
Manny06
- Membre Complexe
- Messages: 2125
- Enregistré le: 26 Jan 2012, 15:24
-
 par Manny06 » 12 Mai 2015, 07:57
par Manny06 » 12 Mai 2015, 07:57
novicemaths a écrit:Bonjour
Le problème est que je ne vois pas comment faire le tableau variation, j'ai oublié de vous dire que f est définie sur

.
A +
Sur cet intervalle x>=0 donc la fonction est croissante
-
novicemaths
- Membre Irrationnel
- Messages: 1110
- Enregistré le: 01 Sep 2014, 10:04
-
 par novicemaths » 13 Mai 2015, 06:09
par novicemaths » 13 Mai 2015, 06:09
Bonjour
Comment pouvez-vous conclure que x>=0 avec

?
A +

-
Ncdk
- Membre Rationnel
- Messages: 758
- Enregistré le: 30 Mar 2014, 19:10
-
 par Ncdk » 13 Mai 2015, 06:35
par Ncdk » 13 Mai 2015, 06:35
novicemaths a écrit:Bonjour
Comment pouvez-vous conclure que x>=0 avec

?
A +
On sait que

mais on sait aussi que la fonction exponentielle est toujours positive, pour tout x. Conclusion ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
avec
et
et
soit
=
=