Etude d'une fraction rationnelle

[Boss_maths]

Bonsoir à tous,

L'étude d'une fonction avec une valeur absolue pour "pimenter" un peu l'exercice.

--- Enoncé ---
1°) Etudier les variations de la fonction :



2°) Construire la courbe représentative de ces variations et tracer les tangentes à cette courbe au point d'intersection avec .

--- Corrigé ---
- Remarque : La fonction risque de présenter une singularité en , reliée à la présence, au numérateur, d'une valeur absolue associée la variable.
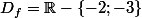
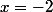
est une fraction rationnelle définie sur :. En effet, son dénominateur est un trinôme qui s'annulle pour ou .
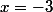
Suivant les valeurs de la variable, l'expression de la fonction aura les 2 écritures suivantes que je choisis pour les différencier :

Si :
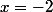
La valeur est une racine commune à chaque trinôme, au numérateur et dénominateur, ce qui pourrait permettre une simplification que je ne ferais pas. En effet, la fonction ainsi simplifiée ne serait pas identique, même si -2 est déjà exclue de
Si : .
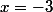
La valeur est une racine commune à chaque trinôme, au numérateur et dénominateur, ce qui pourrait permettre une simplification que je ne ferais pas pour la raison déjà exposée ci-dessus, même si -3 est déjà exclue de .
est définie en mais, pour vérifier sa continuité, je calcule cette valeur dans et et j'ai immédiatement :
=, qui est la même valeur donc, j'en conclue, est continue en .
Recherche des asymptotes à la courbe représentative :
- Rappel du cours :
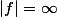
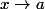
Lorsque lim lorsque , on dit que la droite d'équation est une asymptote à la courbe au voisinage de a.
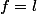
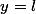
Lorsque lim lorsque , on dit que la droite d'équation est une asymptote à la courbe au voisinage de .
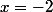
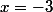
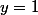
Concernant cette fonction, c'est bien le cas au voisinage des valeurs exclues de : et qui sont des asymptotes verticales. Il s'en suit aussi que : est une asymptote horizontale, car la limite vers est celle du rapport tes termes en , qui est 1.
Pour étudier ses variations, je calcule la fonction dérivée pour et :




Je reprends...

[geegee]

Bonjour,

On peut distinguer deux cas : x négatif, x positif
Puis on peut dérivé ((u/v)'=u'v-uv'/v carré)
Puis on peut factoriser puis étudier le signe

[Boss_maths]

Bonjour,

On peut distinguer deux cas : x négatif, x positif
Puis on peut dérivé ((u/v)'=u'v-uv'/v carré)
Puis on peut factoriser puis étudier le signe

Ben, c'est que je comptais faire avec mes 2 fonctions et ?
Ce n'est pas juste jusque là... ? Où la je viens de tracer la courbe et j'ai un pb... Il me semble qu'elle ne correpond pas au signe de ma dérivée ! En effet, elle doit être croissante pour et Ce n'est pas le cas pour avec son trinôme au numérateur qui a des solutions. Il y a un os quelque part !

Merci et @+ :help:

[Boss_maths]

J'ai des doutes maintenant sur la (non) simplification de la fonction, ce choix que j'aborde au début.

Houston, je ne comprend pas :doute2:

Je me suis planté c'est pareil, mais celà n'explique pas le signe de la dérivée

Merci !

[Doraki]

Tu peux toujours dire que pour tout x dans leur domaine de définition respectifs, f+(x) = l'expression obtenue en simplifiant les facteurs (x+2), et f-(x) = l'expression obtenue en simplifiant les facteurs (x+3).

Si tu gardes à l'esprit que tu peux donner des domaines de définitions explicites pour f,f-,f+ qui retirent -2 et -3, t'as le droit de simplifier leur expression. Le domaine de définition de l'expression il change, mais on s'en fout vu qu'on a décidé avant quel était le domaine de définition de f,f-,f+.

En particulier, quand x tend vers -2, même si f(-2) n'est pas défini, f(x) admet une limite finie, et donc il n'y a pas d'asymptote verticale en -2 (il y en a seulement en -3)

[Boss_maths]

, MA bourde est là au numérateur !
.

Résultat des cour(b)ses, je pouvais simplifier depuis le début !
Maintenant tout s'explique, la fonction est croissante sur tout son domaine, CQFD.

Je m'occupe des tangentes en .
Rappel du cours : l'équation générale de la tangente, en un point a, d'une fonction f, a pour expression : .
ATTENTION, car la fonction possède une singularité pour , 2 tangentes en ce point, un fait qui est a relier aux 2 expressions de la dérivée en ce point.
Calculs des valeurs :
= et et
A partir de ces éléments j'établis les expressions des 2 tangentes associées à :
pour la 1ère :
pour la 2ème :

La courbe représentative : http://cjoint.com/?2mnvCbasxDt
Ouf c'est fini et je pense que c'est bon !?
SVP une petite vérification :++:

@+ Merci !

[Boss_maths]

Tu peux toujours dire que pour tout x dans leur domaine de définition respectifs, f+(x) = l'expression obtenue en simplifiant les facteurs (x+2), et f-(x) = l'expression obtenue en simplifiant les facteurs (x+3).
Si tu gardes à l'esprit que tu peux donner des domaines de définitions explicites pour f,f-,f+ qui retirent -2 et -3, t'as le droit de simplifier leur expression. Le domaine de définition de l'expression il change, mais on s'en fout vu qu'on a décidé avant quel était le domaine de définition de f,f-,f+.

Je résume, une simplification est toujours possible tant que je le fais par des valeurs exclues du domaine et, lorsque je redéfini les 2 fonctions et , je vérifie que ? Je ne sais pas si cette écriture est correcte... la forme.

En particulier, quand x tend vers -2, même si f(-2) n'est pas défini, f(x) admet une limite finie, et donc il n'y a pas d'asymptote verticale en -2 (il y en a seulement en -3)

Oui expliqué ainsi je comprend mieux la subtilité ! Sur le graphique, Geogebra superpose avec la courbe de f. Je pense que c'est normal, des 2 courbes il n'en trace qu'une.

Merci bcp et @+

[sad13]

ne serait pas ce judicieux de placer le post ds la rubrique supérieur?

[Boss_maths]

Ne serait pas ce judicieux de placer le post ds la rubrique supérieur?

Bonsoir,

Et pourtant, cet exercice est extrait d'un livre de 1ère C des années 60 et beaucoup d'autres sont encore plus "corsés".

Merci et @+