Etude d'une fonction exponentielle avec un réel k<e [TS]

[Pierre4]

Bonjour,
j'ai un problème avec 2 questions dans un exercice pourriez-vous m'aider à les résoudre?Je vous donne l'énoncé et vous fais part des réponses trouvées:

Soit k un réel tel que 0Soit f la fonction de la variable réelle x définie sur IR:
f(x)=(2-x)e^(x) -k

1)Déterminer les limites en + et - l'infini

Donc en + l'infini on a lim f(x)=- infini
en - infini on a lim f(x)= -k

2)Trouver les variations de f(x)

On dérive f'(x)=e^x(1-x)
Le signe dépend de 1-x 1-x>0 x<1
La fonction est croissante sur ]-infini;1[ et décroissante sur ]1;+infini[
Avec un maximum atteint en f(1)=e-k

3)a)Établir que l'équation f(x)=0 a deux solutions l'une Bk sur ]1;+infini[ et Ak sur ]-infini;1[.

Sur ]1;+infini[ f est continue(car dérivable), elle est strictement décroissante et les limites en 1 et +infini sont de signes contraires donc d'après le théorème de la bijection.Une seule solution sur ]1;+infini[
Sur]-infini;1[ f continue,croissante et les limites en 1 et -infini sont de signes opposées donc une seule solution sur ]-infini;1[

b)Montrer que:
e^(Ak)-k(Ak)=(e^(Ak)-k)((Ak)-1)
Faire de même pour Bk

Ici je n'arrive pas à prouver j'arrive en développant l'expression de droite à:
e^(Ak)((Ak)-1+k)-k(Ak)
((Ak)-1+k) doit être égal à 1 mais je n'arrive pas à le prouver.

c)Déterminer une valeur approchée de A1, B1 et B2
Ici non plus je ne vois aps comment faire

4)Déterminer le signe de f(x)
Surement postif entre les racine et négatif en dehors

Je vous remercie d'avance pour l'aide que vous allez me consacrer.

[uztop]

Bonjour,

Les questions 1) et 2) sont justes
3)a) c'est bon aussi
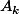
3)b) est une racine donc: (1)
tu dois en fait montrer que

Essaye de développer et réduire cette expression, tu vas tomber sur (1)

3)c) Pour trouver les valeurs approchées, ça peut se faire par dichotomie par exemple, mais je ne sais pas quelle précision on te demande.

4) Oui mais il faut le prouver (en faisant le tableau de variation par exemple)

[Pierre4]

Bonsoir,
merci tout d'abord d'avoir répondu à ma question:).
Donc j'ai développé comme vous me l'aviez dit et je trouve bien le bon résultat c'est à dire:

3.b)
e^(Ak)-k(Ak)=(e^(Ak)-k)((Ak)-1)
e^(Ak)-k(Ak)-(e^(Ak)-k)((Ak)-1)=0
e^(Ak)-k(Ak)-e^(Ak)*(Ak)+e^(Ak)+k*(Ak)-k=0
2e^(Ak)-e^(Ak)*(Ak)-k=0
(2-(Ak))e^(Ak)-k=0
On retrouve bien l'équation d'avant.
3.c)On me demande une valeur approchée à 10^-1 mais comment je les trouve car je ne connais pas la valeur de k donc je ne peux pas rentrer la fonction dans ma calculette pour trouver un encadrement .De plus je ne comprends pas pourquoi on a 3racines et non pas 2.Pourriez-vous m'apporter la réponse?

4)En suite la ça dépend des racines.Il me faudrait la valeur de chaque racine pour déterminer le signe entre les racines.

Je vous remercie d'avance pour votre réponse

[uztop]

donc pour la 3)a) c'est bon
Pour la 3)b), tu connais la valeur de k: A1 c'est pour k=1, A2 et B2 c'est pour k=2
Du coup, ça répond aussi à ta question sur le nombre de racines: il n'y en a bien que 2, mais A1 est pour une équation et A2 et B2 correspondent à une autre équation.
4) Non, pourquoi est ce que tu as besoin de connaitre explicitement les racines ?
Tu sais que et , c'est suffisant

[Pierre4]

Bonsoir, merci tout d'abord d'avoir encore une fois répondu:)
Concernant les racines
pour A1 je trouve -1.2 B1 1.8< B1<1.9
C'est bien ca?Mais je n'ai toujours pas compris l'histoire avec B1 et B2.
J'ai compris que A1 c'est pour une équation et B1 et B2 une autre mais si je prends une valeur de k entre [0;e] la courbe n'intercepte que 2fois l'axe des abscisses.Pourriez-vous m'aider à comprendre svp? :marteau:
Pour la 4 f(x)<0 sur ]-infini;A1]
f(x)>0 sur [A1;B1]
f(x)<0 sur [B1;+infini[
Merci d'avance pour vos réponses