Etude de signe et variations de f

par **SM1** » 14 Déc 2008, 17:30

Bjr,
j'aimerai savoir la méthode pour étudier le signe et faire son tableau de variations de cette fonction f'(x)=-3x^2+6x+24 en calculant le discriminant je trouve 2 et 4 est ce que c'est bon ?

par **Timothé Lefebvre** » 14 Déc 2008, 17:34

Salut, on remarque que

, et que

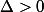
: le sens de variation de ta courbe est donc très facilement connu (c'est du cours).

par **Timothé Lefebvre** » 14 Déc 2008, 17:36

Salut, tu trouves quoi comme discriminant ?

par **SM1** » 14 Déc 2008, 17:36

je c'est que c'est du cours je l'aurais je n'aurais pas demander donc un peu d'aide au moins ce que je fait est ce que c'est bon ?

par **Timothé Lefebvre** » 14 Déc 2008, 17:38

SM1 a écrit:je c'est que c'est du cours je l'aurais je n'aurais pas demander donc un peu d'aide au moins ce que je fait est ce que c'est bon ?

Montre comment tu as fait ?

par **SM1** » 14 Déc 2008, 17:39

je trouve 324 et quand les deux solutions réelles je trouve 2 et 4 ?

par **Black Jack** » 14 Déc 2008, 17:40

SM1 a écrit:Bjr,
j'aimerai savoir la méthode pour étudier le signe et faire son tableau de variations de cette fonction f'(x)=-3x^2+6x+24 en calculant le discriminant je trouve 2 et 4 est ce que c'est bon ?

Attention, on cherche l'expression de f '(x) pour trouver les variations de f(x)

Alors revois la question que tu as posée.

:zen:

par **Timothé Lefebvre** » 14 Déc 2008, 17:42

Ok, je ne trouve pas 4 mais -1 ...

par **SM1** » 14 Déc 2008, 17:43

la question c'est déterminer f'(x) et étudier son signe ce que j'ai fait je trouve - 3x^2+6x+24 la fonction du début c'est -x^3+3x^2+24x-10

par **Timothé Lefebvre** » 14 Déc 2008, 17:44

Ah ben ok !
Je me demandais aussi ce que cette dérivée venait faire ici toute seule.

par **SM1** » 14 Déc 2008, 17:44

-1 comment tu as fait stp ?

par **Timothé Lefebvre** » 14 Déc 2008, 17:46

par **SM1** » 14 Déc 2008, 17:53

je trouve pour x1=-6+racine de 324/2x(-3)=-6+18/-6= 2
et x2=(-6)-racine de 324/ 2x(-3)= -6-18/-6= -24/-6= 4 ?

par **Timothé Lefebvre** » 14 Déc 2008, 17:58

SM1 a écrit:je trouve pour x1=-6+racine de 324/2x(-3)=-6+18/-6= -2
et x2=(-6)-racine de 324/ 2x(-3)= -6-18/-6= -24/-6= 4 ?

^_^J'avais pris

, au temps pour moi.
Par contre

vaut -2 , tu as fait une petite erreur de signe.

par **SM1** » 14 Déc 2008, 18:03

x2 donc c'est bon ? et pour x1 j'ai fait une érreur de signe ou sa ?
racine de 324= 18
-6+18/-6 =
12/-6 =
4x3/-3x2 =
on enlève les 3 il reste 4/2= 2 ?

par **Black Jack** » 14 Déc 2008, 18:05

SM1 a écrit:la question c'est déterminer f'(x) et étudier son signe ce que j'ai fait je trouve - 3x^2+6x+24 la fonction du début c'est -x^3+3x^2+24x-10

Autre technique :

f '(x) = - 3x^2+6x+24
f '(x) = -3 (x^2-2x-8)
f '(x) = -3 ((x-1)²-1-8)
f '(x) = -3 ((x-1)²-3²)

Penser a A²-B² = (A-B)(A+B) ...

:zen:

par **Timothé Lefebvre** » 14 Déc 2008, 18:05

c'est bon oui.

4x3/-3x2 : tu peux enlever quoi ?
Tu as 3 et -3, ça donne -1 !

par **SM1** » 14 Déc 2008, 18:14

ah oui c'est érreur de signe x1 = -2 et x2 = 4 on est d'accord maintenant étudions son signe !

par **SM1** » 14 Déc 2008, 18:32

alors quelqu'un pour m'aider a etudier le signe de ma fonction ?

par **SM1** » 14 Déc 2008, 19:03

? personne pour m'aider svp je dois le rendre demain ?

Etude de signe et variations de f

etude de signe et variations de f

Qui est en ligne