Etude du signe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 13:55
par Marky » 26 Aoû 2009, 13:55
(Re)bonjour à tous, aujourd'hui j'ai un soucis au niveau d'une étude de signe.
Voici ma fonction :
f(x) = x + Racine carrée de (x^2-1)
1. Petite étude du domaine, fonction définie sur l'infini sauf entre -1 et 1 (compris).
2. Tableau histoire d'y voir plus clair

Comment puis-je déterminer le signe de la fonction à l'endroit que j'ai entouré ? Merci d'avance

Edit : Ah, faites pas attention à mon "-" en dessous dans la colonne entourée, c'est un brouillon j'ai laissé ça comme ça...
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Aoû 2009, 14:02
par girdav » 26 Aoû 2009, 14:02
Bonjour.
Tu peux écrire
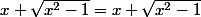\frac{x-\sqrt{x^2-1}}{x-\sqrt{x^2-1}})
que l'on peut simplifier via une identité remarquable bien connue.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Aoû 2009, 14:15
par Ericovitchi » 26 Aoû 2009, 14:15
bof, il va se retrouver avec un dénominateur aussi compliqué que son numérateur actuel.
Tu peux aussi simplement regarder quand est-que

en passant le x de l'autre coté et en élevant au carré. Tu t'apercevra qu'il n'est jamais positif.
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 14:15
par Marky » 26 Aoû 2009, 14:15
Ca me fait effectivement retomber sur
1 / x - Racinée carrée (x^2-1)
Je suis là effectivement sûr que la fonction sera négative en dessous de -1...
Mais par contre je n'ai jamais utilisé cette méthode en cours, est-ce qu'elle ne démature pas l'étude de la fonction ? Enfin, l'étude de la fonction probablement, mais pas l'étude du signe ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Aoû 2009, 14:20
par Ericovitchi » 26 Aoû 2009, 14:20
les deux fonctions sont égales donc toute opération faite sur l'une (dérivée, étude de variation, assymtote, limite, signe,...) vaut pour l'autre aussi. La seule chose qui peut différer c'est le domaine de définition car en créant un dénominateur, on peut introduire des valeurs interdites.
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 14:25
par Marky » 26 Aoû 2009, 14:25
Cela ne modifiera en rien l'étude du signe de la dérivée et de la dérivée seconde ? Ca me semble étrange :o ...
Sinon je me penche sur ta méthode Erico (si je peux me permettre de t'appeler ainsi :p) que j'ai elle effectivement traité en cours d'année. Bonne occasion de revoir ça, ca fait longtemps... Mais l'autre méthode marche également très bien dans le cas du problème actuel non ? (bien que je vais travailler l'autre également, mais je me penche sur une autre fonction pour l'instant)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 26 Aoû 2009, 14:28
par girdav » 26 Aoû 2009, 14:28
Ericovitchi a écrit:bof, il va se retrouver avec un dénominateur aussi compliqué que son numérateur actuel.
Tu peux aussi simplement regarder quand est-que

en passant le x de l'autre coté et en élevant au carré. Tu t'apercevra qu'il n'est jamais positif.
Le dénominateur est négatif. Et dans ce cas il n'y a pas de valeur interdite car

ne s'annule jamais.
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 14:49
par Marky » 26 Aoû 2009, 14:49
Ericovitchi a écrit:Tu peux aussi simplement regarder quand est-que

en passant le x de l'autre coté et en élevant au carré. Tu t'apercevra qu'il n'est jamais positif.
Je comprend le principe mais je ne sais pas comment exprimer ça clairement sur ma feuille =/ Un coup de pouce ?

Pas très clair, hein...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Aoû 2009, 14:55
par Ericovitchi » 26 Aoû 2009, 14:55
non tu as oublié d'élever le -x au carré à droite de l'équation
ça donne

et comme 1 ne peut pas être négatif ....
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 15:43
par Marky » 26 Aoû 2009, 15:43
Ok pour ça. J'ai noté avec la méthode des binômes conjugés par facilité mais je vois l'autre procédé, merci :)
Autre question : si j'ai une A.H en -oo... alors pas d'AO, que ce soit en +oo ou en -oo? Je suppose que non, pas d'AO (vu que l'AH "s'étend" à tout le graphe de la fonction si je puis m'exprimer ainsi), mais j'aimerai être sûr...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Aoû 2009, 15:59
par Ericovitchi » 26 Aoû 2009, 15:59

Tu sembles conclure un peu vite en matière d'asymptote oblique.
Essayes de démontrer par exemple que f(x) - 2x tends vers zéro quand x tends vers l'infini.
Et puis je ne vois pas bien en quoi l'asymptote horizontale s'étendrait "à tout le graphe" ?
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 17:07
par Marky » 26 Aoû 2009, 17:07
Hmm effectivement, j'étais totalement dans l'erreur mais je comprends... Ca va au niveau des asymptotes de cette fonction.
Par contre ici rebelote, je dois faire l'étude du signe de cette fonction :
}{(x^2-1)^3})
Comment je m'y prend au numérateur avec
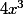
? Pour les racines?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Aoû 2009, 17:23
par Ericovitchi » 26 Aoû 2009, 17:23
tu es sûr de ton écriture cette fois ?
ton polynôme qui est au numérateur n'a qu'une seule racine réelle (qui est autour de -2,035) tu n'as qu'a l'appeler a et faire ton tableau de signes en rajoutant à a les valeurs qui font changer de signe le dénominateur.
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 26 Aoû 2009, 17:29
par Marky » 26 Aoû 2009, 17:29
Comment as-tu trouvé ce nombre ?
Quelle racine obtiens tu pour -8x^3+20x^2-4x-5 ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 26 Aoû 2009, 17:35
par Ericovitchi » 26 Aoû 2009, 17:35
Il suffit d'être équipé par un bon logiciel (en l'occurrence j'utilise Sinequanon qui est gratuit et dont on a souvent parlé sur ce forum).
Pour -8x^3+20x^2-4x-5 = 0 on trouve 3 racines :
-0,38670 ; 0,75998 ; 2,12670
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 27 Aoû 2009, 10:31
par Marky » 27 Aoû 2009, 10:31
(Malheureusement j'ai un mac, il me faudra trouver un autre logiciel)
Je vais laisser ce cube de côté pour un moment, je pense avoir fait une erreur avant et il faudra donc que je regarde ça à nouveau de A à Z pour être sur de mon coup... J'ai quand même déjà 14 pages manuscrites pour le travail que je fais actuellement, ça avance heureusement

.
J'ai un autre soucis aujourd'hui. Je n'arrive pas à trouver mon erreur. Je cherche une asymptote oblique en -oo et je sais que d'après le graphe elle a pour équation y=-x-1, mais je n'arrive pas à ça avec mes calculs que voici :

Désolé pour les maniaques de la propreté ^^'
edit : fonction de base :
}{\sqrt(x^2-x)})

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Aoû 2009, 11:01
par Ericovitchi » 27 Aoû 2009, 11:01
si tu veux montrer que -x-1 est asymptote pour x tendant vers - l'infini, il faut calculer la limite de f(x)+x+1 et montrer qu'elle tends vers zéro. Or je n'ai pas vu ce calcul là dans ta feuille ?
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 27 Aoû 2009, 11:22
par Marky » 27 Aoû 2009, 11:22
On m'a appris à appliquer la méthode suivant pour trouver une AO en -oo :
1. Lim -oo f(x)/x (Si on trouve un réel autre que o, on l'appelle a)
2. Lim -oo f(x)-a.x (Si on trouve un réel, on l'appelle b)
Et on trouve notre A.O ayant pour équation y=a.x+b
Ici je trouve a = -1
Donc je calcule Lim -oo (fx) + x

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 27 Aoû 2009, 11:27
par Ericovitchi » 27 Aoû 2009, 11:27
Très bonne méthode.
Tu as fait la moitié et maintenant il faut donc calculer f(x)+x et montrer que ça tends vers -1 donc.
-
Marky
- Membre Naturel
- Messages: 43
- Enregistré le: 15 Mai 2009, 16:21
-
 par Marky » 27 Aoû 2009, 11:28
par Marky » 27 Aoû 2009, 11:28
Et donc mon problème est que je tombe sur le résultat que j'ai inscris sur ma feuille, alors que sur le graphe l'asymptote est clairement en y=-x-1 =/
edit pour au dessus : oui je l'ai fais, j'ai modifié ce qu'il fallait en rouge, mais le résultat pour moi reste que ça tend vers 0. D'où l'erreur que je n'arrive pas à cibler :triste:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités




