Etude de fonction
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 13:45
par Amiss » 01 Jan 2010, 13:45
Bonjour, je dois prouver que f(x)=x²+ 1/V(x+1)=2 a une solution est la déterminer sur [0:4]
Ensuite, jai un petit probleme pour étudier le signe de cette fonction qui est la dérivée de f(x) (je ne suis meme pas sur de l'avoir bien dérivé :triste: ) :
2x - 1/[(2x+2)V(x+1)]
Jai pensé a tout mettre sur le meme dénominateur mais la soustraction me gene toujours.
V = racine de
Pouvez vous m'aider sil vous plait?
Merci
-
Noemi
- Membre Complexe
- Messages: 3241
- Enregistré le: 20 Oct 2007, 16:09
-
 par Noemi » 01 Jan 2010, 13:54
par Noemi » 01 Jan 2010, 13:54
Bonjour,
Etudie les variations de la fonction.
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 13:57
par Amiss » 01 Jan 2010, 13:57
Je sais bien quil faut que jétudie les variations!! Mais mon soucis et davoir le signe de la dérivée et la soustraction me gene
-
Noemi
- Membre Complexe
- Messages: 3241
- Enregistré le: 20 Oct 2007, 16:09
-
 par Noemi » 01 Jan 2010, 14:11
par Noemi » 01 Jan 2010, 14:11
Cela correspond à la première question de l'exercice ou il y avait des questions avant ?
si non,
Tu prends l'équation de départ et tu réduis au même dénominateur.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 14:23
par Ericovitchi » 01 Jan 2010, 14:23
Oui étudies la fonction

Sa dérivée 2 x-1/(2 (x+1)^(3/2)) va te montrer qu'elle décroit depuis -1 et atteint un minimum vers x=0.192 qui vaut -1.04 donc négatif puis remonte vers l'infini. Elle coupe donc l'axe 2 fois.
(Pour les calculer précisément il faudrait l'écrire
=1)
, élever au carré pour enlever la racine
 (2-x^2)^2-1=0)
(degré 5 quand même !)
mettre ça en produit de facteurs =
 (x^3+2 x^2-x-3))
puis trouver les racines. la première qui est solution de l'équation du second de gré est facile
}{2})
~-0.618 mais elle n'est pas entre [0,4], l'autre est plus dure à trouver x~1.1479 )
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 14:24
par Amiss » 01 Jan 2010, 14:24
Il n'y a quune seule question, je dois déterminer la solution de f(x)=0 je sais bien quil faut mettre sous le meme dénominateur mais je ny arrive pas, je ne sais comment transformer de facon correcte ma dérivée (elle t elle bonne?) pour en étudier son signe
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 14:28
par Amiss » 01 Jan 2010, 14:28
Ericovitchi merci pour tes précieuses indications, cela signifie donc que me dérivé est fausse, le soucis cest que je ne sais comment trouver LA bonne dérivée sans faire d'ereur (jai déja passé beaucoup de tps sur le calcul de la dérivée :( ..) Quelle formule dois-je utilisé? car pour le x² on est daccord que cest 2x, mais lautre partie est un quotient mélangé a une composé??

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 14:30
par Ericovitchi » 01 Jan 2010, 14:30
Si, elle a l'air juste ta dérivée, c'est la même que la mienne.
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 14:41
par Amiss » 01 Jan 2010, 14:41
Mais je ne comprends pas l'exposant (3/2)...
edit :
Ma dérivée est : 2x - 1/[(2x+2)V(x+1)] et non pas 2x - 1/[(x²- 2)V(x+1)]
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 14:44
par Amiss » 01 Jan 2010, 14:44
De plus, que fait on du 2x??? pourquoi ne l'étudie t on pas?
EDIT :
d'autre part,
je ne comprends pas trop pourquoi est ce que pour les calculer précisément il faudrait l'écrire
=1)
, d'ou sort le =1?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 14:48
par Ericovitchi » 01 Jan 2010, 14:48
C'est pareil d'écrire
^{\frac{3}{2})
ou
\sqrt{x+1})
Tu n'es peut-être pas habitué aux exposants fractionnaires ?
en fait
^{\frac{1}{2}})
Ca permet par exemple de dériver plus simplement car
^{\frac{1}{2})
peut se dériver comme un
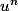
donc en
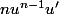

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 14:54
par Ericovitchi » 01 Jan 2010, 14:54
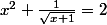
C'est bien ça ton équation de départ ?
Donc
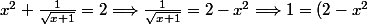 \sqrt{x+1})
Produit en croix
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 14:57
par Amiss » 01 Jan 2010, 14:57
Les exposants fractionnaire.. non, jai jamais compris clairement cela..
Et oui cest bien mon équation de départ
Ma dérivée est : 2x - 1/[(2x+2)V(x+1)] et non pas 2x - 1/[(x²- 2)V(x+1)]
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 15:13
par Amiss » 01 Jan 2010, 15:13
Aaaaaa!! je crois avoir compris, mais en fait, dans mon énoncé, je dois utilisé le TVI pour prouver l'unique solution dans l'intervalle, par conséquent, je doit faire un tableau de variations de f mais le gros soucis et que je n'arrive a étudier le signe de la dérivée

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 16:53
par Ericovitchi » 01 Jan 2010, 16:53
Tu n'as pas vraiment besoin de t'embêter avec la dérivée. Tu sais que le résultat est à peu près ~1.1479 donc tu te mets un peu avant 1,14 et tu montres que la fonction est négative, un peu après (à 1,15 par exemple) et tu remarques que la fonction est positive et avec le théorème des valeur intermédiaire, tu en conclus qu'il y a une racine entre ces deux valeurs.
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 18:07
par Amiss » 01 Jan 2010, 18:07
Ah daccord! Je vois je vois..
Mais ensuite pour trouver la racine exacte de ceci :
)
sur [1;4] comment dois-je procéder?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 19:24
par Ericovitchi » 01 Jan 2010, 19:24
C'est possible avec les formules de Cardan mais on ne te demande pas de donner la formulation exacte de la solution.
Utilises une méthode approchée comme celle de Newton.
Cela dit si ça t'amuse la solution exacte vaut :
})
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 20:40
par Amiss » 01 Jan 2010, 20:40
Oo! Le soucis cest que ma prof demande de déterminer la solution est non pas un encadrement comme pour les autre question..
"déterminer l'unique solution sur [0;4] de l'aquation x²+1/(V(x+1)=2"
Cest normal?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 01 Jan 2010, 21:55
par Ericovitchi » 01 Jan 2010, 21:55
Et bien tu lui dis que c'est x~1.1479
-
Amiss
- Membre Naturel
- Messages: 24
- Enregistré le: 16 Mar 2008, 18:12
-
 par Amiss » 01 Jan 2010, 22:33
par Amiss » 01 Jan 2010, 22:33
Daccord daccord! Merci énormément pour tout mais peut etre quelle attend de nous la formule de cardan??
Au fait la formule de Cardan moi javais appris quelle servait pour les complexe, valeurs irréelles non?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 73 invités

=1) , élever au carré pour enlever la racine
, élever au carré pour enlever la racine (2-x^2)^2-1=0) (degré 5 quand même !)
(degré 5 quand même !) (x^3+2 x^2-x-3)) puis trouver les racines. la première qui est solution de l'équation du second de gré est facile
puis trouver les racines. la première qui est solution de l'équation du second de gré est facile }{2}) ~-0.618 mais elle n'est pas entre [0,4], l'autre est plus dure à trouver x~1.1479 )
~-0.618 mais elle n'est pas entre [0,4], l'autre est plus dure à trouver x~1.1479 )