Etude de fonction

[b747400]

Problème résolu

[b747400]

Voici mes réponses:

Partie A:

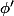1)Etudions les variations de (x)

(x)=
(x)=

Dressons le tableau de variation de (x)



avec =0 et =0.9

2) Montrons que la fonction s'annule exactement une fois sur l'intervalle [2;20]. Indiquons la valeur arrondie à une décimale de ce nombre.

est une fonction strictement croissante sur [2;20]. Puisque est uen fonction continue sur cet intervalle et que 0 soit un réel compris entre et alors l'équation a une solution unique sur cet intervalle car est une fonction monotone.

[fonfon]

Salut,

avec =0 et =0.9

2) Montrons que la fonction s'annule exactement une fois sur l'intervalle [2;20]. Indiquons la valeur arrondie à une décimale de ce nombre.

est une fonction strictement croissante sur [2;20]. Puisque est uen fonction continue sur cet intervalle et que 0 soit un réel compris entre et alors l'équation a une solution unique sur cet intervalle car est une fonction monotone.

tes valeurs et ne sont pas bonnes

2) la redaction un peu plus rigoureuse

tu peux ecrire:
sur [2,20] f est continue et strictement croissante avec et , elle realise une bijection de [2,20] sur ,0 appartiant à donc a une solution sur [2,20]

si tu appelles la valeur qui annule la fonction
on a soit

comme est croissante sur [2,20] , 5.3<<5.4

[b747400]

Je vois mais j'ai un peu de mal à suivre. D'où viennent tes 5.3 et 5.4 ? merci de m'éclairer

[fonfon]

Je vois mais j'ai un peu de mal à suivre. D'où viennent tes 5.3 et 5.4 ? merci de m'éclairer

il faut te servir de ta calculatrice il faut que tu trouves un encadrement de la valeur qui annule ta fonction sur [2,20]

et d'apres l'ennoncé

Indiquons la valeur arrondie à une décimale de ce nombre

donc tu calcules qui est proche de 0 mais negatif et tu calcules qui est proche de 0 mais qui est positif

donc tu sais que ta valeur qui annule ta fonction , moi je l'ai appelé ,est compris entre ces 2 valeurs -0.035<<0.27 donc 5.3<<5.4

[b747400]

Ah il s'agissait d'un encadrement, je vois merci pour ta réponse. En ce qui concerne la question 3. je suppose que le signe de la fonction est positif sur . Par conséquent, je reprends le tableau précédent en y ajoutant la ligne du signe de , ce qui me donne:



n'est ce pas ?

[fonfon]

Ah il s'agissait d'un encadrement, je vois merci pour ta réponse. En ce qui concerne la question 3. je suppose que le signe de la fonction est positif sur . Par conséquent, je reprends le tableau précédent en y ajoutant la ligne du signe de , ce qui me donne:



n'est ce pas ?

non, c'est pas bon

tu sais que ta fonction s'annule pour un cetain appartenant [2,20]
donc sur est negative et sur est positive

[b747400]

Ce qui donne cela:

[fonfon]

non, ne fait pas ton tableau on ne te demande pas les variations, on te demande le signe de sur [2,20] ce que j'ai ecris est suffisant

[b747400]

Mais alors pourquoi est-il demandé de récapituler tous ces résultats dans un tableau ? :-s

[fonfon]

1.Etudier les variations de la fonction puis dresser son tableau de variation.
2.Montrer que la fonction s'annule exactement une fois sur l'intervalle . Indiquer la valeur arrondie à une décimale de ce nombre.
3.En déduire le signe de la fonction sur l'intervalle

je ne vois pas ou il est demandé de recapituler tout dans un tabeau

[b747400]

Excuse moi je n'ai pas noté toute la consigne:
En déduire le signe de la fonction phi(x) sur l'intervalle [2;20] et récapituler ces résultats dans un tableau

[b747400]

désolé pour l'erreur

[fonfon]

bon ben tu peux faire un tableau de ce style



bon il est pas terrible le tableau mais je pense que ça te donne une idée

[b747400]

Pour la Partie B j'ai fais ceci:

1)a) Montrons que la dérivée f' de f a le même signe que sur ]2;20]






Comment montrer ensuite que f' de f a le meme signe que sur ]2;20] ?

[fonfon]

tu as dû te tromper dans ta dérivée








or (x-2)²>0 sur ]2,20] donc f'(x) est du signe de

jerepasse tout à l'heure je dois m'absenter

[b747400]

Réponse à la question 1b) je reprends les résultats de la 1a) et je cherche pour quelle valeur f s'annule n'est ce pas ?

[fonfon]

re,

tu sais que f'(x) est du signe de sur ]2,20]
or
est negative sur donc f'(x)0 sur

donc f est decroissante sur et f est croissante sur ]


pour la limite en 2+, je trouves+ inf essaie de trouver ce resultat

je dois partir pour ce soir mais demain matin je serais là donc essaie d'avancer je corrigerais à moins que quelqu'un prenne le relais

A+

[b747400]

2ln(2) > 0
En 2+ : lim xln(x)/(x-2) -> +oo
En 2- : lim xln(x)/(x-2) -> -oo
En 2 : lim xln(x)/x - 2 -> ln(2)

Pour la question 2, je ne vois pas trop ce qu'il faut faire

[fonfon]

Salut,

2ln(2) > 0
En 2+ : lim xln(x)/(x-2) -> +oo
En 2- : lim xln(x)/(x-2) -> -oo
En 2 : lim xln(x)/x - 2 -> ln(2)

tu etudies ta fonction sur ]2,20] donc on veut juste la limite en 2+ soit



donc