étude de fonction.

[levisionniste]

Bonjour à tous,

il m'est demander dans un exercice d'effectuer l'étude complète de la fonction f(x)= e^(-1/x)

-dom de f
-racine
-parité
-asymptote
-dérive 1
-dérivé 2
-graphique


Domaine de définition:


} - inf ; 0 { U } 0 ; + inf {



racine de la fonction:


pas de racine


parité de la fonction:


ni paire ni impaire


asymptotes:

av: limite de x tend -+0 de e^(-1/x) = e^(+-inf)=+inf

donc il existe une av en x= 0

ah: limite de x tend +-inf de e^(-1/x) = e^(-+o) = 1

il existe une av en y= 1

ao : pas de ao

dérivée

1) e^(-1/x) * (1/x^2)

2) (e^(-1/x) / x^4) - (2e^(-1/x)/x^3)



pourriez vous me dire si j'ai des fautes je vous prie.

[Deluxor]

Bonsoir!



OK pour le domaine de définition de la fonction, pour la recherche des racines, pour l'étude de la parité, et pour les dérivées première et seconde.

Pour les asymptotes, je récapitule et/ou rectifie ce que tu as écrit :

, donc la courbe représentative de admet la droite d'équation 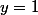comme asymptote horizontale en et en .

, donc la courbe représentative de admet la droite d'équation comme asymptote verticale.

[levisionniste]

je vous remercie

[geegee]

Bonjour à tous,

il m'est demander dans un exercice d'effectuer l'étude complète de la fonction f(x)= e^(-1/x)

-dom de f
-racine
-parité
-asymptote
-dérive 1
-dérivé 2
-graphique


Domaine de définition:


} - inf ; 0 { U } 0 ; + inf {

ou R\{0}

racine de la fonction:


pas de racine


parité de la fonction:


ni paire ni impaire


asymptotes:

av: limite de x tend -+0 de e^(-1/x) = e^(+-inf)=+inf
lim(x->0+)e^(-1/x) = 0
im(x->0-)e^(-1/x) = +infini
donc il existe une av en x= 0

ah: limite de x tend +-inf de e^(-1/x) = e^(-+o) = 1

il existe une av en y= 1

ao : pas de ao

dérivée

1) e^(-1/x) * (1/x^2)
f'(x)> 0 donc f est croissante sauf en x=0.

2) (e^(-1/x) / x^4) - (2e^(-1/x)/x^3)



pourriez vous me dire si j'ai des fautes je vous prie.