Etude de fonction numérique Cm

[AMARI]

Bonjour à Tous,

Dans la mesure de vos possibilités, bien vouloir m'aider pour répondre à une dernière question :

Démontrer que tous les points ou cette fonction accepte une dérivée nulle appartient à une fonction (P) indépendante de "m" en écrivant son équation.

f(x)=e^(-2x)-(1+m) e^(-x)+m

f'(x)=e^(-2x)+me^(-x)

Je vous Remercie Vivement

[AMARI]

Rebonjour à Tous,

Erreur de ma part:

f'(x)=-2e^(-2x)+(1+m)e^(-x)
Et Merci à Tous

[AMARI]

Bonjour à Tous,

Pour plus de précision, on cherche l'équation de la fonction de l'ensemble des extrémums.

Merci Bien

[Ben314]

Salut,
En résolvant l'équation tu trouve une unique solution dépendant bien sûr de : (modulo que soit >-1).
En reportant cette valeur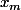 dans l'équation de la fonction tu trouve un dépendant bien sûr lui aussi de .
Ce que tu cherche, c'est une certaine fonction indépendante de telle que, pour tout on ait .
Et ça ne pose pas de difficulté vu que tu connait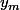 en fonction de et que la relation donnant 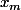en fonction de s'inverse très facilement pour donner en fonction de .

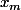A toi de jouer . . .

[mathou13]

Bonjour,

f(x)=e^(-2x)-(1+m) e^(-x)+m

f'(x)=-2e^(-2x)+(1+m)e^(-x) posons X=e^(-x)
=0 <-> -2X^2+X+mX=0
Delta=1+8m>=0
m>=-1/8
X1=(-1+-racine(1+8m))/-4
Xm=(1+racine(1+8m))/4
D'où m=.... en fonction de Xm(=e^(-xm))
On a m en fonction de xm donc f(xm)= ...que fonction de xm en remplaçant m par xm.

[Ben314]

-2X^2+X+mX=0
Delta=1+8m>=0
m>=-1/8
X1=(-1+-racine(1+8m))/-4
Xm=(1+racine(1+8m))/4

Un seul mot : CHAPEAU !!!
Déjà, d'utiliser une formule "toute faite" style pour résoudre une équation de la forme , c'est pas triste, mais en plus se débrouiller, au final, pour ne même pas obtenir la solution qui sautait aux yeux dés le départ, là, c'est le bouquet . . .

[AMARI]

Bonjour à Tous,

Dans un premier temps, je tiens à Remercier vivement, Mrs Ben314 et mathou 13,pour le temps consacré aux détails du règlement de ce problème.
Je vous informe à la fin que j'ai trouvé la fonction suivante :

g(x)= -〖(1-e^(x))^2/e^(2x)
c a d
moins (1 - expo (x)) diviser par expo (x) , le tout au carré et que j'ai vérifié avec m=1 , m=2, m=3 et qui a donné de bon résultats.

Je vous Remercie encore.