Etude des fonctions numeriques

[nytcopalaa]

Bonjour, j'espère que vous allez bien

Ma question est sur la monotonie et la composée d'une fonction.
Je sais que une fonction est croissante ssi ses composantes ont la meme monotonie et elle est decroissante ssi ses composantes n'ont pas la meme monotonie.
Existe-il des cas dont ces 2 propriétés ne sont pas valables ?

à titre d'exemple: soit f(x)=h(g(x)) avec f(x)=x-4*racine(x-3) et g(x)= racine (x-3 ) et h(x)=x²-4x+3
Sur [3;7] : h et g sont croissantes sur cet intervalle, or f est decroissante



Cordialement,

[nytcopalaa]

Vous pouvez les representer graphiquement dans le site suivant :https://www.desmos.com/calculator

[hdci]

Bonjour,

elle est decroissante ssi ses composantes n'ont pas la meme monotonie.

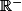
Sur , prenons u la fonction exponentielle (croissante), v la fonction carrée (décroissante), alors est croissante. Pourtant u et v n'ont pas la même monotonie...

[mathelot]

Bonjour,

elle est decroissante ssi ses composantes n'ont pas la meme monotonie.

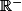
Sur , prenons u la fonction exponentielle (croissante), v la fonction carrée (décroissante), alors est croissante. Pourtant u et v n'ont pas la même monotonie...

??

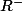
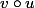
u est croissante sur à valeurs positives, v est croissante sur , est croissante sur

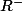
On note que la composée d'une fonction croissante et d'une fonction décroissante est décroissante.

[hdci]

Oups oui j'ai tout mélangé je crois... puisque u est à valeur dans R+...

Il faut vite oublier ce que j'ai écrit...