être au clair avec les probabilités conditionnelles!

[tist]

Bonjour, voici un exercice énoncé comme ceci lors d'un concours et qui fait appel aux probabilités conditionnelles, et il y a une subtilité dans la formulation je trouve:

EXERCICE: Paul est dans un club de foot. On désigne par A l'évènement: "Paul jouera au prochain match" et on estime que la probabilité de cet évènement est P(A)=0,6.
Max est dans le même club de foot. On estime que les informations qu’il fournit sont fiables à 70% , c’est-à-dire que, en moyenne, sur 100 affirmations, 70 seront justes.
Si Max dit que Paul jouera le prochain match, quelle est la probabilité qu'il le joue réellement?
On désignera par B l’évènement : « Max dit que Paul jouera le prochain match »

REPONSE: il est clair qu'on cherche P(A|B). (Probabilité de A sachant B)

1) Ma première réponse est d'utiliser la formule de Bayes: P(A|B)= P(B|A) * P(A)/P(B) et que:
- P(A)=0,6
- P(B|A)= 0,7: (en effet 70% des affirmations de Max sont justes, cela signifie que dans l’univers où A est réalisé [cad ou Max joue le match de samedi prochain], il y a 70% de chances que Max dise qu’il le jouera et 30% de chances qu'il dise le contraire)
- P(B) se calcule par la formule des probabilités totales:
P(B)=P(A)*P(B|A) + P(non A)*P(B|non A) = 0,6 * 0,7 +0,4*0,3
et on termine le calcul on trouve environ 77%

2) on me souffle que la réponse est tout simplement P(A|B) = 0,7 puisque 70% des affirmations de Max sont justes!

Et avec la réflexion je dois avouer que je ne suis plus si sûr de moi et que si j'ai opté pour la réponse n°1 c'est peut-être inconsciemment que la n°2 me semble trop facile.
cela n'utiliserait même pas P(A), c'est très bizarre. Et en même temps je dois bien avouer que l'explication soulignée me convainc plutôt plus que celle en gras, elle est moins alambiquée!

Qu'en pensez-vous? Cela me fait pensez aux exercices sur les tests : la probabilité qu'un individu est atteint d'une pathologie sachant que le test est positif n'est pas la même que la probabilité que le test soit positif sachant qu'il est atteint
Mais dans notre cas je trouve ça plus ambigu!

merci!

[zygomatique]

salut

la probabilité que Max joue le prochain match est la somme des probabilités que :

Max joue le prochain match et Paul l'a prédit
Max joue le prochain match et Paul ne l'a pas prédit

de toute façon on te dit que la probabilité de l'événement A : "Max joue le prochain match" est 0,6

donc la réponse est 0,6

sinon la probabilité que Max joue le prochain match sachant que Paul dit qu'il le jouera est 0,7

[tist]

bonjour merci mais désolé tu ne réponds pas vraiment à la question, tu répètes la réponse 2 mais l'intéressant ici c'est d'expliquer pourquoi la 1 ne va pas et d'essayer de voir où l'énoncé veut en venir.

Il est certain que la réponse n'est pas 0,6 , que c'est bien une probabilité conditionnelle qui est demandé ici. La réponse 2 semble évidente mais il y a quelque chose de bizarre.

[beagle]

Si tu fais l'arbre suivant, les probas conditionnelles devraient s'éclairer:

L'évènement B est point de départ.
Il y a deux branches:
-p(B) proba que Max dise Paul jouera
- et la branche 1-p(b), proba que max dise Paul ne jouera pas

de p(b) part deux branches
une de proba 0,7 il a raison paul jouera
une de proba 0,3 Paul ne jouera pas

de 1 - (pb) part également deux branches:
une de proba 0,7 il a raison Paul ne jouera pas
une de proba 0,3 il a tort, Paul jouera.

Et comme le dit zygomatique:
Paul jouera dans deux cas:
p(b) x 0,7
et 1- p(b) x0,3
cette somme vaut 0,6, on trouve un p(b) = 3/4

Et de cet arbre tu peux retrouver proba que Paul joue sachant que Max a dit qu'il jouerait.
Sachant que Max a dit Paul jouera nous positionne sur la première branche p(b), et lorsqu'on est là (on sait que l'on est là, c'est cela le sachant que), ben effectivement la proba que Paul joue est la triviale branche à 0,7.

[Ben314]

Salut,
Le problème vient (comme à peut près toujours en proba) du fait qu'il manque une information cruciale dans l'énoncé pour faire des calculs, à savoir le problème de l'indépendance des différentes propositions.

En fait, si
A = "Paul joue le match"
B = "Max dit que Paul jouera le prochain match"
C = "Paul dit la vérité"
Alors la proba. à calculer est

Si on suppose que A et B sont indépendants alors il n'y a (quasi) rien à calculer : p(AnB)=P(A).p(B) donc p=p(A)=0.6 et on se fiche de p(B) ou de p(C).

Mais, on peut aussi supposer que les truc indépendants sont A et C (c'est personnellement ce qui me semble le plus plausible).
Ca conduit à écrire que donc que via l'indépendance de A et C.
On a alors en considérant que p(C)=0,7 (*)

Bilan, perso, je voterais plutôt pour 0.78, mais au niveau "carré-carré", la seule réponse valable, c'est "on ne peut rien déduire vu qu'on ne sait pas qui est indépendant de qui"

(*) Sans parler du fait que le 0,7 de l'énoncé peut s'interpréter soit comme étant (ce qui a ma préférence) soit comme étant

[tist]

merci à vous. Quelques commentaires:

1) beagle: ok mais tu fais toute une circonvolution, ton point de vue se résume en une phrase:
de p(b) part deux branches
une de proba 0,7 il a raison paul jouera
une de proba 0,3 Paul ne jouera pas
ainsi pour toi P(A|B) = 0,7 et je crois qu'on peut s'arrêter là!

2) ben 314: merci effectivement tu soulèves des points intéressants.
Mais:
- la seule chose dont je suis (quasi...) sûr c'est que la probabilité qu'on cherche n'est pas 0.6

- C'est soit le 0,77 qu'on trouve tous les deux, moi en parlant plus de probabilités conditionnelles car il me semble que c'est l'esprit du sujet

- soit le 0,7

la différence tient vraiment dans l'interprétation de " sur 100 informations 70 seront justes".
Le plus tentant est de dire: bon c'est pas compliqué, sur 100, 70 sont justes, donc si Max dit que paul jouera, alors 7 chances sur 10 qu'il jouera vraiment

L'autre, est de dire: dans le cas où A est réalisé , la proba que Max dise qu'il joue est la probabilité qu'il dise la vérité, et que ça c'est universellement 0,7: en effet cela revient à dire que le fait de dire ou non la vérité est indépendant du sujet abordé.
dans ce modèle ça justifie la réponse qui donne 0,77 mais j'ai du mal, avec ce modèle, à expliquer que l'autre réponse, 0,7, est fausse, car le " sur 100 informations 70 seront justes", est assez implacable...

3) qui peut peut-être nous éclairer: dans le sujet il y a en fait une deuxième question:

Luc est aussi au club de foot et ses informations sont fiables à 90%.
On considère que les affirmations de Luc et de Max sont indépendantes
On note D l'évènement "Luc dit que Paul jouera".
Si Max dit que Paul jouera et Luc dit qu'il ne jouera pas, quelle est la probabilité qu'il joue?

Alors:
*dans le cadre de mon interprétation, en refaisant Bayes + proba totales, j'arrive à conclure en faisant bien attention que pour moi B et D sont indépendants conditionnellement à A mais pas indépendants tout court sinon cela n'a pas de sens (en effet si B est réalisé, ça augmente la proba que A le soit et donc diminue le fait que D le soit. en revanche à A fixé, les avis sont indépendants)

* dans le cadre de l'autre interprétation, je n'arrive pas à calculer ce P(A sachant B inter non C)!

Merci en tout cas à vous!

[Ben314]

Avant de regarder ton truc, je vais faire un "bilan" des interprétations vu que ma remarque (*) précédente est pas si claire que ça...

A = "Paul joue le match" ; clairement connu (=0,6)
B = "Max dit que Paul jouera le prochain match" ; a priori inconnu.
C = "Max dit la vérité" ; ; pas clair si c'est connu.
+ Une proba. dont le sens n'est pas clair...

Comme l'ensemble des possibilités est partitionné en 4 par , , , , 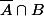il faut 3 infos. pour tout déduire sachant qu'on en a une seule de "sûre", .

Interprétation 1) On considère que le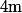 est la proba qu'un truc (quelconque) soit vrai lorsque Max dit que c'est vrai ce qui signifie que mais aussi que ça nous fait nos 2 infos de plus.
On en déduit que donc que , mais aussi que donc que .
Cela montre déjà qu'on a
Sinon, du fait que on déduit que et donc que cette interprétation ne peut avoir de sens que si et que est entre et 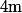ce qui est bien le cas ici. (on peut aussi avoir et 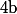quelconque).
On peut maintenant calculer toutes les proba qu'on veut et voir en particulier que :
- (évidement trivial vu l'interprétation faite)
- A et B sont indépendants a=m (faux ici)
- A et C sont indépendants a=1/2 ou m=1 (faux ici)
- B et C sont effectivement indépendants.

Interprétation 2) On suppose uniquement que il manque une info. et on peut par exemple considérer que l'info "manquante" concerne l'indépendance des évènements:
2.1) Si on suppose A et B indépendants (moyennement raisonnable), on peut tout calculer et on a trivialement .
2.2) Si on suppose A et C indépendants (assez raisonnable), on peut tout calculer et après calculs on trouve ici
2.3) Si on suppose B et C indépendants (semble bizarre comme hypothèse), on retombe assez clairement sur l'interprétation 1)

Conclusion : dans tout les cas d'interprétation on a donc, contrairement à ce que je disait dans le (*) de mon précédent post, ce n'est pas là que se situe la différence mais bien uniquement dans le choix de qui est indépendant de qui, sachant que l'indépendance de B et C qui semble difficile à justifier comme "interprétation de base" se trouve être une conséquence de l'interprétation "plus naturelle" .
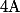Je n'ai pas regardé les interprétations "mixtes" du style mais et 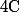indépendants.

Sinon, concernant l'autre question, si on prend
D = "Luc dit que Paul jouera le prochain match"
E = "Luc dit la vérité"
Tu interprète comment la phrase "On considère que les affirmations de Luc et de Max sont indépendantes" ?
Comme voulant dire que B et D sont indépendant ou alors que C et E sont indépendants ? (ou autrement ?)

[tist]

Merci!
Il va falloir que je réfléchisse tranquillement à ça ce que je ne peux pas faire tout de suite, mais pour ta question: pour moi, "les affirmations de Luc et Max sont indépendantes" signifie:
P([B inter D] sachant A) = P(B sachant A) * P(D sachant A).
idem en remplaçant A par son complémentaire (comme pour D ou B bien sûr)

En revanche je pense que dire que P(B inter D) = P(B) * P(D) est un faux-sens.

[Pseuda]

Si on prend à la lettre ce qui est écrit : "On estime que les informations que Max fournit sont fiables à 70% , c’est-à-dire que, en moyenne, sur 100 affirmations, 70 seront justes", cela rend l'événement "Paul jouera au prochain match" indépendant de ce que Max dit. D'ailleurs, cela rend indépendant ce que Max dit de tous les événements dont il parle.

Dans ce contexte, je dirais donc :
- si on ne sait pas ce que Max a dit, la probabilité de réalisation de l'événement "Paul jouera au prochain match" est de 0,6
- si on sait ce qu'il a dit, cette probabilité est de 0,7.

[Pseuda]

De manière plus rigoureuse :

A = "Paul jouera le prochain match" ; p(A) = 0,6
B = "Max dit que Paul jouera le prochain match"
M = "Max dit la vérité" ; p(M) = 0,7

On considère que "Max dit que Paul jouera le prochain match", donc p(B)=1 (c'est un fait certain).

Dès lors, p(A\B) = p(M\B) (M dit la vérité en disant que Paul jouera le prochain match) = p(M) (car M c B et p(B)=1) = 0,7

Mais on fait peut-être une erreur en affirmant cela : p(A) (Paul joue le prochain match) = p(M\B) (M dit la vérité en disant que Paul jouera le prochain match).

Maintenant, si on a :

C = "Luc dit que Paul jouera le prochain match"
L = "Luc dit la vérité" ; p(L) = 0,9

alors : P(A) = p(M\B ou L\C) (M dit la vérité en disant que Paul jouera le prochain match, ou Luc dit la vérité en disant que Paul jouera le prochain match, ou les deux).
Ces 2 événements ne sont pas indépendants ni incompatibles. C'est plus compliqué...

[Pseuda]

En prenant les choses de manière exhaustive, on peut exprimer ce problème avec un diagramme de Venn avec les 3 événements plus hauts :

A = "Paul jouera le prochain match" ; p(A) = 0,6
B = "Max dit que Paul jouera le prochain match" p(B)= inconnu
M = "Max dit la vérité" ; p(M) = 0,7.

Il y a 8 régions avec une probabilité totale de 1 :
p() = x, p() = y, p() = z , p() = t, les probabilités des autres régions sont égales à 0.

On aboutit à un système de 3 équations à 4 inconnues :
x+y=0,6
x+t=0,7
x+y+z+t=1

D'où une infinité de solutions. En considérant que des événements sont indépendants :

* si on suppose que A et M sont indépendants (le plus plausible), on a : x = (x+y)(x+t) et on aboutit à = (bravo Ben !)

* si on suppose que B et M sont indépendants, on aboutit à : = 0,7

* si on suppose que A et B sont indépendants, on aboutit à = 0,6.

Si je ne me suis pas trompée dans les calculs. J'ai du mal à le comprendre de manière logique. Notamment que le cas de = 0,7 correspond à B et M indépendants.

Comme quoi, avec les probabilités, il faut être très prudent et ce qui paraît logique n'est pas forcément la bonne réponse...

[beagle]

Et ben alors on va prier pour que A, B et M ne soient pas indépendants en mème temps!

Perso je suis un peu paumé.
Faut me redonner des cubes ou des haricots ...

B," max dit quelque chose":
on note k quand il dit que Paul jouera et i quand il dit Paul ne jouera pas.
Ainsi après 1000 matchs j'ai une série de 1000:
kkikiikki...

a mes yeux, lorsque j'analyse l'ensemble des k, ben 70% sont bons Paul a bien joué lorsque j'analyse les i, 70% des i sont bons, Paul n'a pas joué.
J'imagine bètement que j'ai le droit de dire que M ne dépend pas de B.

Par contre si j'ai 70% de bonnes réponses sur les 1000, avec un % de bons différent quand c'était des k versus les i, ben alors j'aurais dit que M dépend de B
Mais ce cas contrevient à l'énoncé qui dit :"en moyenne, sur 100 affirmations, 70 seront justes"
sur 100 affirmations jouera pas, ce n'est pas 70 de juste.

[beagle]

"Si je ne me suis pas trompée dans les calculs. J'ai du mal à le comprendre de manière logique. Notamment que le cas de p(A|B) = 0,7 correspond à B et M indépendants."

Ben moi c'est l'inverse où j'ai du mal.
A et B indépendants, un prédicteur indépendant de ce qui va advenir.
Cela me semble incoompatible avec un M à 0,7.
Connaitre la prédiction, connaitre B ne renseigne en rien sur A c'est le prédicteur nul.
Prenons un prédicteur sur et certain, Max est l'entraineur, c'est lui seul qui décide.
Alors connaitre B avec un M de 1 c'est connaitre A avec une proba de 1
p(A/B) = 1
lorsque p(A/B)=p(A) c'est que le prédicteur ne prédit rien.

[beagle]

" J'ai du mal à le comprendre de manière logique. Notamment que le cas de p(A|B) = 0,7 correspond à B et M indépendants."

c'est pourtant le cas le plus évident et c'était ta première réponse sur ce fil.
Admettons 1000 matchs,
B = max dit paul jouera se note k, jouera pas se note i,
alors on a une série de kkikikik qui est B
en dessous on note V ou F pour M , V= max a bon F max a faux
Lorsque l'on reprend tous les k qui sont en fréquence de 0,7, idem à tous les i qui sont en fréquence de 0,7,
alors on peut dire que M ne dépend pas de B.
Je ne vois pas pourquoi cela n'est pas le cas le plus basique,
Ben314 dit trivial il me semble.
Dans le diagrame de Venn:
Paul jouera-Max a dit Paul jouera = 0,525
Paul jouera-Max a dit Paul jouera pas=0,075
Paul jouera pas -max a dit jouera pas =0,175
Paul jouera pas - max a dit paul jouera =0,225

Paul jouera = 0,525+0,075=0,6
Paul jouera pas=0,225 + 0,175= 0,4
Proba max dira Paul jouera est 0,75

pourquoi cela n'est pas le cas le plus simple?

[Pseuda]

" J'ai du mal à le comprendre de manière logique. Notamment que le cas de p(A|B) = 0,7 correspond à B et M indépendants."

c'est pourtant le cas le plus évident et c'était ta première réponse sur ce fil.
Admettons 1000 matchs,
B = max dit paul jouera se note k, jouera pas se note i,
alors on a une série de kkikikik qui est B
en dessous on note V ou F pour M , V= max a bon F max a faux
Lorsque l'on reprend tous les k qui sont en fréquence de 0,7, idem à tous les i qui sont en fréquence de 0,7,
alors on peut dire que M ne dépend pas de B.
Je ne vois pas pourquoi cela n'est pas le cas le plus basique,
Ben314 dit trivial il me semble.
Dans le diagrame de Venn:
Paul jouera-Max a dit Paul jouera = 0,525
Paul jouera-Max a dit Paul jouera pas=0,075
Paul jouera pas -max a dit jouera pas =0,175
Paul jouera pas - max a dit paul jouera =0,225

Paul jouera = 0,525+0,075=0,6
Paul jouera pas=0,225 + 0,175= 0,4
Proba max dira Paul jouera est 0,75

pourquoi cela n'est pas le cas le plus simple?

Je comprends ce que tu veux dire (si on répète souvent l'expérience avec B et M indépendants, on aura effectivement B et M indépendants). Mais intuitivement = 0,7 correspond plus à A et M indépendants qu'à B et M indépendants. Il y a là un biais (qui doit se situer dans les interprétations de Ben314) que je ne m'explique pas logiquement.

A et M indépendants apparaît le plus indiscutable (qu'auraient à voir Paul qui joue un match avec une probabilité de 0,6, avec Max qui dit la vérité dans 70% des cas de manière générale), qui ne se connaissent peut-être même pas, sachant qu'on ne connait pas la probabilité de B qui peut être n'importe quoi ?

Ok pour = 0,7 est le plus simple ; mais le problème donné en TS n'aurait pas d'intérêt (trivial), il faut bien faire quelques calculs. Donc dans ce problème, il est sous entendu que A et M sont indépendants et que =.

Il est à noter que A et B indépendants est impossible. Après calculs, on aurait une probabilité négative pour y (c'est à dire que Paul joue le match avec Max qui ment et qui dit qu'il ne le jouera pas) = - 0,3, ce qui est assez logique compte tenu que Max dit la vérité dans 70% des cas, donc ce qu'il dit n'est de toute façon pas neutre, et que si on a A, on a forcément un lien avec B.

Enfin, A, B et M ne peuvent pas être en même temps tous les 3 indépendants 2 à 2 (logique), et qu'ils peuvent être tous dépendants 2 à 2 (sans qu'il n'y en ait 2 indépendants) avec une infinité de solutions.

[beagle]

Ben314:
"Sinon, concernant l'autre question, si on prend
D = "Luc dit que Paul jouera le prochain match"
E = "Luc dit la vérité"
Tu interprète comment la phrase "On considère que les affirmations de Luc et de Max sont indépendantes" ?
Comme voulant dire que B et D sont indépendant ou alors que C et E sont indépendants ? (ou autrement ?)"

Si on prend C et E indépendants, et idem question 1 ils sont indépendants de A,
alors on a cas favorable = 0,6x0,7x0,1
sur cas cas totaux = 0,6x 0,7x 0,1 + 0,4xx0,3x0,9

[beagle]

D'une façon générale.
Je suis d'accord pour dire que la solution triviale n'était pas celle attendue,
mais cela on le sait d'autant plus lorsque l'on connait les questions suivantes.
Une réponse basique en question 1 d'un exo de 6 à 8 questions , c'est possible.
Maintenant si l'exo avait deux questions, peu probable de demander un élément de l'énoncé en question 1.

Alors vous nous dites c'est pour faire du calcul.
Du calcul de proba conditionnelle.
Très bien , mais alors serait intéressant de savoir de quoi on parle.
Que signifie concrètement l'indépendance de ceci et cela.
pas seulement pour avoir un résultat.
Le corrigé de Ben314 est très intéressant, mais il faut reconnaitre que si Ben314 maitirse également ce qui est concrètement sous-jaccent, ben c'est pas si facile je trouve.
Mème si je ne suis pas trop dans le coup en ce moment, je trouve qu'il faut sérieusement des repères pour savoir à quoi on joue.
genre dire qu'un prédicteur est indépendant de la prédiction, hum c'était dur à imaginer ...

Voilà, bel exo grace à Ben314 pour qui veut bosser ce sujet.
Mais je le répète s'agit pas de faire des calculs mais bien de savoir à quoi on joue, à quoi correspondent les différents calculs ...

[Pseuda]

L'exercice n'est toujours pas résolu tant qu'on n'a pas compris pourquoi la probabilité de A sachant B est égale à celle de M quand B et M sont indépendants, et non pas quand c'est A et M qui sont indépendants.
Quand j'aurai plus de temps...

[beagle]

L'exercice n'est toujours pas résolu tant qu'on n'a pas compris pourquoi la probabilité de A sachant B est égale à celle de M quand B et M sont indépendants, et non pas quand c'est A et M qui sont indépendants.
Quand j'aurai plus de temps...

B et M indépendants
M c'est vrai ou faux, c'est V ou F
B c'est dit jouera = B , dit jouera pas = non B
L'indépendance oblige d'avoir dans l'ensemble des V et dans l'ensemble des F,
la mème proportion de B et non B.
S'il en était autrement = déséquilibre quelconque, alors connaitre V ou connaitre F, renseignerait sur B ou nonB, il y aura plus ou il y aurait moins de B que dans le p(B) total.
Donc il y a 70% des B dans les V, et 30% des non B dans les V
et 70% des B dans les F et 30% des non B dans les F.

70% des B dans les V, donne proba de Paul jouera sachant B = 0,7

[beagle]

Versus A et M indépendants:
j'ai mème proportion de M 0,7 et 0,3 dans les A paul joue que dans les A Paul ne joue pas.

Les vrais dans les A, c'est quand B max dit il va jouer, et c'est vrai
les M F= faux dans joue pas de A c'est quand Max dit va jouer et c'est faux il ne jouera pas

donc cas favorables = 0,6 x0,7
cas totaux = 0,6x 0,7 + 0,4x 0,3
cela donne 0,7/0,9= 7/9