Estimation sur echantillon

[Severine_b21]

salut à tous,

ça fait quelques jours que je buche sur ces problèmes et je dois l'avouer c'est l'enfer, je mélange toutes les formules.

on veut estimer la moyenne M d'une variable aléatoire X suivant une loi normale, de variance connue = 6.25 à l'aide d'un échantillon de taille n = 100 valeurs indépendantes. La moyenne de l'échantillon est 4.3.

1°. Construire un intervalle de confiance avec un coefficient de confiance a x=0.95

2°. Comment construire un tel intervalle, si l'on ne connait pas la variance X, mais seulement la varance empirique S2 = 0.76 de l'échantillon.
MERCI

[Isomorphisme]

Bonjour,

Je pense que cette question n'est pas de niveau lycée (d'après ce que j'ai vu tu es en DAEU).
Dans ton cours, tu n'as pas des formules ? car c'est typiquement du cours
Si la variance est connue, il faut utiliser un fractile de la loi normale, sinon de la loi de Student. Regarde dans ton cours et sinon reposte. Bon courage !

[Severine_b21]

Bonjour,

Je pense que cette question n'est pas de niveau lycée (d'après ce que j'ai vu tu es en DAEU).
Dans ton cours, tu n'as pas des formules ? car c'est typiquement du cours
Si la variance est connue, il faut utiliser un fractile de la loi normale, sinon de la loi de Student. Regarde dans ton cours et sinon reposte. Bon courage !

merci, j'ai bidouillé avec plusieurs formules, on verra bien!

[Isomorphisme]

Eh bien pour vérification :
1 - Cas où la variance est connue : l'intervalle de confiance au risque vaut :

avec bien sûr,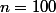 , , et (fractile d'ordre 0.975 de la loi normale centrée réduite). Ce qui donne
2 - Cas où la variance est inconnue. On estime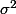 par 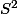. Il vient l'intervalle de confiance :

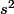avec et (fractile d'ordre 0.975 de la loi de Student à 99 ddl). D'où l'intervalle de confiance : . Rmq : la valeur de semble louche.
J'espère ne pas avoir fait d'erreur.

[Severine_b21]

Eh bien pour vérification :
1 - Cas où la variance est connue : l'intervalle de confiance au risque vaut :

avec bien sûr, , , et (fractile d'ordre 0.975 de la loi normale centrée réduite). Ce qui donne
2 - Cas où la variance est inconnue. On estime par . Il vient l'intervalle de confiance :

avec et (fractile d'ordre 0.975 de la loi de Student à 99 ddl). D'où l'intervalle de confiance : . Rmq : la valeur de semble louche.
J'espère ne pas avoir fait d'erreur.

merci la premiere j'ai trouve mais pas la seconde!