DM / 1 ére spé Maths ( à rendre Lundi )

[mmaarrggauuxx]

Bonjour , je suis bloquée avec le DM que je dois faire , il y a certaines questions que je n'arrive pas à faire , pourriez vous m'aidez , merci (qst 2 et 4)

• Une entreprise produit entre 0 et 50 balançoires par jour . Le coût de fabrication de x balançoires , en Euros , est donné par la fonction suivante :
f : [ 0;50 ] --> R
x --> f(x) = x² + 230x + 325

• Chaque balançoires est vendu 300 € et toute la production est vendue .
1) Exprimer le bénéfice B(x) réalisé par l'entreprise en fonction de x. (Déjà répondu)
2)Étudier les variations de la fonction B .
3) En déduire le bénéfice maximal réalisé par l'entreprise. (Déjà répondu )
4)Combien de balançoires l'entreprise doit -elle produire et vendre pour être rentable ?

[hdci]

Bonjour,

Qu'as-tu essayé de faire ? Par exemple, comment peux-tu répondre à la question 3 sans avoir traité la question 2 (puisque la quesiton 3 est "en déduire", c'est qu'on utilise le résultat de la question 2).

Qu'as-tu trouvé pour la fonction B ?

[mmaarrggauuxx]

La première question j'ai pu y répondre en disant :
B(x) = 300x - ( x² + 230x + 325 )
B(x) = 300x - x² - 230x - 325
B(x) = 70x - x² - 325

- La question 2 , je ne sais pas du tout .
- La question 3 , j'ai déduis toute seule en disant :
B(35) = (70 × 35) -35² -325
B(35) = 2450 -1225-325
B(35) = 900 € / J
Le bénéfice maximal réalisé par l'entreprise est de
900€ par jour avec 35 balançoires.
(J'ai essayé avec 50 bal' / 40 bal' /15 ' et le
bénéfice le plus élevé est celui avec 35
balançoires)
- La question 4 , je sais pas comment faire .
Voilà merci !

[hdci]

Pour la question 1, c'est correct.
Pour la question 3, comment as-tu trouvé x=35 : application d'un résultat de cours ? Par tâtonnement ou analyse graphique avec un logiciel / une calculatrice ?

Pour commencer, prends l'habitude d'écrire le polynôme en puissance décroissante ; ce n'est pas obligatoire, mais cela va forcément être en phase avec ce que tu as vu en cours :


C'est donc un polynôme du second degré, et tu as forcément vu en cours le sens de variation d'un tel polynôme: dans le cas général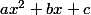 l'orientation de la parabole dépend du signe de ... ?

pour la quatrième question, là aussi tu as dû voir en cours comment on résout l'inéquation

[mmaarrggauuxx]

Merci pour vos conseils ,
La question 3 , je l'ai fait par calculatrice , mais je note tous mes calcules sur la feuille que je vais rendre le jour J .
Oui nous sommes en train de voir ça en cours (polynômes du second degrés ) , à quels question cela peut-il m'aider ?

[hdci]

Pour les questions 2 et 3, le cours doit te donner cette indication :

Dans le cas général , la courbe représentative est une parabole orientée "vers le haut" si et "vers le bas" si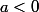
Pour s'en souvenir, on peut considérer le moyen mnémotechnique suivant : on n'aime pas les nombres négatifs car ils sont source d'erreurs de signes ; donc si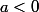 la parabole "pleure" et si la parabole "sourit"

Dans ton cas, le coefficient devant le carré est (car ) donc négatif et la parabole "pleure" : ce qui indique que la courbe monte puis descend, elle est croissante à gauche et décroissante à droite.

Le sommet est atteint pour la valeur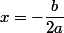 avec ici 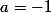et 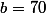, donc pour 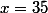comme ce que tu avais trouvé avec la calculatrice (sauf qu'avec la calculatrice tu n'aurais pas fait la différence entre 35 et 35,001 par exemple...)

Le sommet correspond au maximum de la fonction (car la parabole "pleure" ou parce que le tableau de variations indique "croissant" puis "décroissant"), d'où la question 3 "en déduire..."

Enfin, pour la question 4, la règle à retenir est la suivante : s'il y a des racines, la fonction est du signe de "à l'extérieur des racines". On détermine donc les racines en calculant le discriminant et ici comme a=-1, la fonction est négative "à l'extérieur des racines", donc positive "entre les deux racines".
Pour une résolution graphique (donc imprécise), la fonction est positive si la courbe est au-dessus de l'axe des abscisses, donc on cherche quelles sont les intersections avec l'axe des abscisses.