DL et équivalent
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
par mimix » 02 Nov 2010, 10:49
Bonjour à tous,
Je viens de commencer les DL, et j'ai besoin d'aide pour comprendre l'égalité suivante:
J'ai:
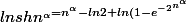.<br /> = n^{\alpha}.(1-ln2/n^{\alpha} + o(1/n^{\alpha})))
J'ai essayé d'effectuer un DL en utilisant ln(1+x) au premier ordre, mais j'ai une exponentielle. Quelqu'un peut-il m'expliquer comment on obtient cette égalité?
J'ai une autre question aussi:
^(1/n) = n(1-ln2/alpha.n^{\alpha} + o(1/n^\{alpha})).)
Pourquoi a-t-on un ln2/alpha.n^(alpha)??
Merci beaucoup!!
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 02 Nov 2010, 11:33
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
par mimix » 02 Nov 2010, 14:09
Je ne vois pas en quoi ça peut m'aider.. ?
C'est le DL qui me bloque, qu'est-ce qu'on a fait pour arriver à cette égalité?
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 02 Nov 2010, 14:44
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
par mimix » 02 Nov 2010, 15:22
Pourquoi ce serait pas un petit o(x) ?
le rapport ln(1+e-2x)/x tend vers 0, donc x domine ln(1+e-2x)?
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
par mimix » 02 Nov 2010, 15:29
Ah nan c'est bon!
Merci beaucoup arnaud32! :lol3:
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 02 Nov 2010, 15:34
si c'est un o(1/x) en +inf c'est a fortiori un o(x) :-)
si g(x)=o(1/x) alors xg(x) tend vers 0 en +inf
et g(x)/x=(xg(x))*(1/x²) qui tend lui aussi vers 0 en +inf ...
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
par mimix » 02 Nov 2010, 16:02
J'ai encore une question:
quand on le met en ^(1/x), pour passer de:
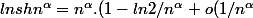<br /><br />(lnshn^{\alpha})^{1/\alpha} = n( 1- ln2/\alpha.n^{\alpha} + o(1/n^{\alpha}))
on a effectuer un DL?
c'est le
qui me pose problème
-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
par arnaud32 » 02 Nov 2010, 16:45
)^{1/a}=(n^a(1-\frac{ln(2)}{n^a}+o(\frac{1}{n^a}))^{1/a}=n*(1-\frac{ln(2)}{n^a}+o(\frac{1}{n^a})^{1/a})
(1-x)^b = 1-bx+o(x) au voisinage de 0 donc:
}{n^a}+o(\frac{1}{n^a})^{1/a}=1-\frac{1}{a}(\frac{ln(2)}{n^a}+o(\frac{1}{n^a}))+o(\frac{ln(2)}{n^a}+o(\frac{1}{n^a})))
}{n^a}+o(\frac{1}{n^a})^{1/a}=1-\frac{ln(2)}{a*n^a}+\frac{1}{a}(o(\frac{1}{n^a}))+o(\frac{ln(2)}{n^a}+o(\frac{1}{n^a})))
or
)+o(\frac{ln(2)}{n^a}+o(\frac{1}{n^a}))=o(\frac{1}{n^a}))
d'ou ton resultat.
-
mimix
- Membre Naturel
- Messages: 74
- Enregistré le: 02 Nov 2010, 10:38
-
par mimix » 02 Nov 2010, 16:47
Merci, c'était juste pour confirmer!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
