Équivalence logique

[Ilyaskilango]

(x,y) appartient à R^2
En utilisant un raisonnement par équivalence établir l'équivalence suivante
[x+rac(x^2+1)]×[y+rac(y^2+1)]=1 equivale x+y=0

[Ilyaskilango]

J'ai essayer tt les méthode que je sais mais j'ai pas pu le démontrer

[Ben314]

Salut,
Perso, ce que je ferais, c'est de partir de là : et de résoudre l'équation en , c'est à dire de faire comme si était connu.

Est-ce que tu saurait comment procéder pour résoudre par exemple ?
Si oui, ben tu fait exactement la même suite d'opération, mais avec à la place du .

P.S. : Il y aurait des méthodes bien plus rapides que par équivalence algébrique "pure et dure", par exemple avec avec un calcul direct pour l'implication x+y=0 => . . . et une petite étude de fonction pour la réciproque.

[capitaine nuggets]

Salut !

Posons et ; on peut utiliser les quantités conjuguées : par exemple donc puisque (à vérifier) (et ) ne s'annule(nt) jamais, on a :



c'est-à-dire . En soustrayant membre à membre l'égalité à l'inégalité , on a 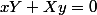. Or puisque 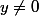(pourquoi ?) . Cela revient donc à dire (je te laisse vérifier) :



J'ai abrégé les calculs, mais je ne suis pas sûr de savoir si la méthode que je te propose est plus rapide que celle de Ben314...

[Ben314]

J'ai abrégé les calculs, mais je ne suis pas sûr de savoir si la méthode que je te propose est plus rapide que celle de Ben314...

C'est peut-être un peu plus court, j'en sais rien. Mais ce qui m’embête un peu, c'est plutôt par rapport à la directive donnée demandant d'utiliser "uniquement un raisonnement par équivalence".
Là, partant de l'hypothèse (une unique équation), tu fabrique une deuxième équation, puis tu soustrait une des équation à l'autre et, bien évidement, ce que tu obtient après soustraction, à priori, c'est uniquement une déduction de l'hypothèse donc pas une équivalence (*) et ça t'oblige à vérifier à la fin que la valeur que tu obtient est bien solutions du problème initial.
Cette vérification est évidement complètement immédiate, mais, à mon sens, elle fait qu'on ne peut plus vraiment dire que tu as procédé "uniquement par équivalence".

Mais bon, une directive du type "En utilisant un raisonnement par équivalence . . .", c'est pas non plus forcément super archi clair ce que ça signifie. (et on peut éventuellement dire qu'on pas lu ou mal lu ou pas compris la directive... )

(*) c.f. le fameux "paradoxe du collégien" consistant à partir de X^2+X+1=0, à multiplier par X, puis à retrancher l'équation de départ où ça créé bien évidement une "solution parasite" à savoir X=1.

[Ben314]

Par équivalence "le plus pur possible", à mon avis, ça donnerais ça :

(1) Le dénominateur est toujours non nul, car en multipliant par le conjugué, ça donne systématiquement 1.
(2) En multipliant par le conjugué puis en retranchant des deux cotés.
(3) Deux réels sont égaux si et seulement si leurs carrés sont égaux et qu'ils sont de même signe.
(4) Le même argument qu'en (1) montre que n'est jamais nul.

Bref, c'est quand même plutôt plus long...

[Ilyaskilango]

Merci ben ton aide est très précieux et merci à capitaine logique aussi