Bonjour
Je me demandais si on a x appartient à R
15.x^4 - 26.x^2 + 11 = 0 et x^2 = 1
Est-ce que c'est logiquement équivalent à
x^2 = 1 ?
Équivalence équation
10 messages
- Page 1 sur 1
Re: Équivalence équation
Bonsoir
ah non...résous ton équation bicarrée, tu vas voir...
ah non...résous ton équation bicarrée, tu vas voir...
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Équivalence équation
Salut !
Nommons et
et  respectivement l'ensemble des solutions des équations
respectivement l'ensemble des solutions des équations 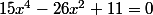 et
et 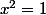 . Posons
. Posons 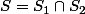 l'ensemble des solutions des deux équations.
l'ensemble des solutions des deux équations.
Dire que est solution de
est solution de 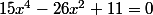 et
et 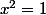 revient à dire que
revient à dire que 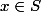 .
.
Or l'ensemble des solutions de l'équation
des solutions de l'équation 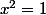 est facile à trouver et sachant que
est facile à trouver et sachant que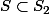 , on peut pas avoir d'autres solutions en plus que celle appartenant à
, on peut pas avoir d'autres solutions en plus que celle appartenant à  . Il suffit donc en fait de vérifier quelles solutions appartenant à
. Il suffit donc en fait de vérifier quelles solutions appartenant à  appartiennent aussi à
appartiennent aussi à  .
.
Autre méthode : en remarquant que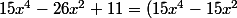-(11x^2-11)) , montre que
, montre que 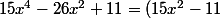(x^2-1)) .
.

Nommons
Dire que
Or l'ensemble
Autre méthode : en remarquant que
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Équivalence équation
Bonjour,
x^2=1 <-> x=+-.... (car un carré n'est pas strictement négatif dans R).
donc S={.... ; ....}.
x^2=1 <-> x=+-.... (car un carré n'est pas strictement négatif dans R).
donc S={.... ; ....}.
Re: Équivalence équation
re
j'avais manifestement mal compris la question !
j'avais manifestement mal compris la question !
Pour mettre une image, vous pouvez aller sur https://postimages.org/fr/
Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.

Vous choisirez ce qu'ils appellent le lien direct (lien de la seconde ligne), que vous placerez entre les balises Img.
Re: Équivalence équation
les 2 propositions sont équivalentes : NON.
Si proposition2 est vraie, alors proposition1 est vraie.
Mais l'inverse n'est pas vrai.
Regarde la fin du message de Capitaine Nuggets.
Si proposition2 est vraie, alors proposition1 est vraie.
Mais l'inverse n'est pas vrai.
Regarde la fin du message de Capitaine Nuggets.
Re: Équivalence équation
???????lyceen95 a écrit:les 2 propositions sont équivalentes : NON.
Si proposition2 est vraie, alors proposition1 est vraie.
Mais l'inverse n'est pas vrai.
Lorsque tu as deux propositions P et Q avec P qui implique Q (*) alors il est bien clair que la proposition (P et Q) et complètement équivalente à la proposition P seule.
Par exemple (x>3 et x>5) est totalement équivalente à x>5.
(*) et ici, on constate trivialement que, si x^2=1 alors 15.x^4 - 26.x^2 + 11 = 15-26+11 = 0
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Équivalence équation
Ben314 a écrit:???????lyceen95 a écrit:les 2 propositions sont équivalentes : NON.
Si proposition2 est vraie, alors proposition1 est vraie.
Mais l'inverse n'est pas vrai.
Lorsque tu as deux propositions P et Q avec P qui implique Q (*) alors il est bien clair que la proposition (P et Q) et complètement équivalente à la proposition P seule.
Par exemple (x>3 et x>5) est totalement équivalente à x>5.
(*) et ici, on constate trivialement que, si x^2=1 alors 15.x^4 - 26.x^2 + 11 = 15-26+11 = 0
Dans le cas général (comme tu viens de le faire avec P et Q ) comment ça se démontre que c'est équivalent à P ?
Re: Équivalence équation
Ben c'est complètement con :
- Si (P et Q) est vraie, alors P est évidement vraie (sans avoir besoin d'hypothèse supplémentaire).
- Réciproquement, si P est vraie et qu'on suppose que P implique Q alors Q est aussi vraie donc (P et Q) est vraie.
Bilan : lorsque P implique Q, les propositions P et (P et Q) sont équivalentes.
Et je reprécise que c'est un truc absolument crétin de la vie courante : si tu lit sur l'étiquette de tes graines de carottes qu'il faut une terre à au moins 10 degré pour que ça germe et sur celle des graines de tomates qu'il faut au moins 15 degré pour que ça germe, ben pour que les deux germent il faut (et il suffit) que les tomates germent.
- Si (P et Q) est vraie, alors P est évidement vraie (sans avoir besoin d'hypothèse supplémentaire).
- Réciproquement, si P est vraie et qu'on suppose que P implique Q alors Q est aussi vraie donc (P et Q) est vraie.
Bilan : lorsque P implique Q, les propositions P et (P et Q) sont équivalentes.
Et je reprécise que c'est un truc absolument crétin de la vie courante : si tu lit sur l'étiquette de tes graines de carottes qu'il faut une terre à au moins 10 degré pour que ça germe et sur celle des graines de tomates qu'il faut au moins 15 degré pour que ça germe, ben pour que les deux germent il faut (et il suffit) que les tomates germent.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
