Equations trigo
38 messages
- Page 2 sur 2 - 1, 2
Oui, soit 3 angles soit 3 côtés égaux.
Je te propose de montrer que les 3 côtés sont égaux :
Pour cela on peut définir un repère (O,i,j) pour lequel O est le centre du cercle trigonométrique. Dans ce repère, quelles sont les coordonnées des 3 points (donne des noms à tes points)? Comment calculer les longueurs des 3 cotés en utilisant ces coordonnées?
PS : Sinon une méthode plus rapide serait d'utiliser une propriété des angles au centre dans un triangle équilatérale, mais si tu ne vois pas de quoi je parle, on reviendra plus tard la-dessus.
Je te propose de montrer que les 3 côtés sont égaux :
Pour cela on peut définir un repère (O,i,j) pour lequel O est le centre du cercle trigonométrique. Dans ce repère, quelles sont les coordonnées des 3 points (donne des noms à tes points)? Comment calculer les longueurs des 3 cotés en utilisant ces coordonnées?
PS : Sinon une méthode plus rapide serait d'utiliser une propriété des angles au centre dans un triangle équilatérale, mais si tu ne vois pas de quoi je parle, on reviendra plus tard la-dessus.
bombastus a écrit:Oui, soit 3 angles soit 3 côtés égaux.
Je te propose de montrer que les 3 côtés sont égaux :
Pour cela on peut définir un repère (O,i,j) pour lequel O est le centre du cercle trigonométrique. Dans ce repère, quelles sont les coordonnées des 3 points (donne des noms à tes points)? Comment calculer les longueurs des 3 cotés en utilisant ces coordonnées?
PS : Sinon une méthode plus rapide serait d'utiliser une propriété des angles au centre dans un triangle équilatérale, mais si tu ne vois pas de quoi je parle, on reviendra plus tard la-dessus.
Alors je propose un premier point a ( 0;1) un autre a ( cos 5pi/6 ; sin 5pi/6) et enfin un a (cos pi/6 : sin pi/6) et pour calculer la longeur de chaque coté cette formule
d:racine((x2-x1)²+(y2-y1)²)
Mais je me demande si il n'y pas moyen d'y arrivé avec l'equation du cerle vu qu'on a les coordonnées du centre du cercle on peut donc trouver le rayon qui serait egales au cotes du triangle mais je ne suis pas sur...
dri-dry a écrit:Alors je propose un premier point a ( 0;1) un autre a ( cos 5pi/6 ; sin 5pi/6) et enfin un a (cos pi/6 : sin pi/6) et pour calculer la longeur de chaque coté cette formule
d:racine((x2-x1)²+(y2-y1)²)
Donne des noms différents à tes points! :hein:
Sinon le premier est faux : ce n'est pas (0;1) (je te rappelle que l'angle est 3pi/2).
dri-dry a écrit:Mais je me demande si il n'y pas moyen d'y arrivé avec l'equation du cerle vu qu'on a les coordonnées du centre du cercle on peut donc trouver le rayon qui serait egales au cotes du triangle mais je ne suis pas sur...
Et pourquoi le rayon du cercle serait égal au côté du triangle???
bombastus a écrit:Donne des noms différents à tes points! :hein:
Sinon le premier est faux : ce n'est pas (0;1) (je te rappelle que l'angle est 3pi/2).
Et pourquoi le rayon du cercle serait égal au côté du triangle???
Oui desoler pour le sommet de langle 3pi/2 c'est (0;-1) et avec ca je peux calculer les distances? les 2 autres points sont bon?
bombastus a écrit:Elle ne ressemble pas à une simple puissance...
D'une manière générale, lorsque le x est en puissance, mieux vaut passer par l'exponentielle.
OK
si je fais la drivée seconde j'obtient
x^x(2lnx+(1/x))
mais apres je dois etudier la concavitée dans le domaine des positifs mais je nai aucune idée de comment resoudre l'equation
x^x(2lnx+(1/x))=0
je ne sais meme pas par ou commencer... :mur:
En fait je crois que j'avais mal compris ta question de départ...
Mais si j'ai bien compris, pour toi:
(x^x)' = x^xlnx
c'est bien cela? Ou as-tu vu cela?
En fait tu es en quel classe?
En terminale en france, on voit que pour étudier la fonction a^x, le plus simple est de passer par l'exponentielle et le logarithme :
on a :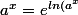} = e^{x ln(a)})
C'est ce que j'ai adapté ici :
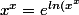} = e^{x ln(x)})
Est ce que tu comprends cela?
Mais si j'ai bien compris, pour toi:
(x^x)' = x^xlnx
c'est bien cela? Ou as-tu vu cela?
En fait tu es en quel classe?
En terminale en france, on voit que pour étudier la fonction a^x, le plus simple est de passer par l'exponentielle et le logarithme :
on a :
C'est ce que j'ai adapté ici :
Est ce que tu comprends cela?
bombastus a écrit:En fait je crois que j'avais mal compris ta question de départ...
Mais si j'ai bien compris, pour toi:
(x^x)' = x^xlnx
c'est bien cela? Ou as-tu vu cela?
En fait tu es en quel classe?
En terminale en france, on voit que pour étudier la fonction a^x, le plus simple est de passer par l'exponentielle et le logarithme :
on a :
C'est ce que j'ai adapté ici :
Est ce que tu comprends cela?
Enfaite comme question jai une etude de fonction dc je dois dérivé cette fonction
autre méthode
dri-dry a écrit:2sin²x+sinx=1
L'équation du second degré est bien. voilà une autre méthode:
on termine en égalisant deux sinus.
38 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
