Equations
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
lepomédu11
- Membre Naturel
- Messages: 20
- Enregistré le: 08 Nov 2006, 16:31
-
 par lepomédu11 » 08 Nov 2006, 18:14
par lepomédu11 » 08 Nov 2006, 18:14

Si vous avez une idée ne serait-ce que pour me lancer
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 08 Nov 2006, 18:16
par Elsa_toup » 08 Nov 2006, 18:16
Il suffit de remplacer x par les valeurs qu'on te propose ! Si tu trouves pareil à droite et à gauche, c'est gagné !
-
Imod
- Habitué(e)
- Messages: 6482
- Enregistré le: 12 Sep 2006, 11:00
-
 par Imod » 08 Nov 2006, 18:18
par Imod » 08 Nov 2006, 18:18
Une idée toute bête , remplacer x par les solutions proposées et regarder si les deux membres sont égaux . Sinon tu peux aussi commencer par réduire l'équation pour limiter les calculs .
Imod
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 08 Nov 2006, 18:20
par Zebulon » 08 Nov 2006, 18:20
Bonsoir,
pour vérifier qu'un nombre est solution d'une équation, on remplace x par ce nombre dans le membre de gauche de l'équation et on calcule, puis on remplace x par ce nombre dans le membre de droite de l'équation et on calcule. Le nombre est solution si et seulement si le membre de droite est égal au membre de gauche.
Ici, pour déterminer si -2 est solution de l'équation
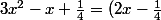^2)
,
on calcule d'une part
^2-(-2)+{1\over4})
,
d'autre part
-{1\over4})^2)
,
est-ce égal ? Donc -2 est-il solutioon de l'équation ?
Même chose pour

.
-
cLa!r3
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Oct 2006, 22:10
-
 par cLa!r3 » 08 Nov 2006, 18:24
par cLa!r3 » 08 Nov 2006, 18:24
Bonsoir lepomé ^^,
Elsa toup à raison,
il te suffit de calculer séparément :  - pour x = -2
- pour x = -2^2 - (-2) + \frac {1}{4})
= 0
Puis ^2) - toujours pour x = -2
- toujours pour x = -2 - \frac {1}{4})^2)
Si tu trouve deux résultats équivalent pour x=-2, alors -2 est solution de l'équation.------------------------------------------------------------------------
De même pour x=
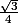
Ciao !
-
lepomédu11
- Membre Naturel
- Messages: 20
- Enregistré le: 08 Nov 2006, 16:31
-
 par lepomédu11 » 08 Nov 2006, 18:35
par lepomédu11 » 08 Nov 2006, 18:35
Je trouve:
A gauche:
57/4
A droite:
56.25/4
Je sens qu'il y a une faute
-
Elsa_toup
- Membre Irrationnel
- Messages: 1491
- Enregistré le: 04 Nov 2006, 16:29
-
 par Elsa_toup » 08 Nov 2006, 18:41
par Elsa_toup » 08 Nov 2006, 18:41
Non, je ne trouve pas comme toi. Je te onseille de garder les résultats sous forme fractionnaire (avec des /4)
-
cLa!r3
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Oct 2006, 22:10
-
 par cLa!r3 » 08 Nov 2006, 18:50
par cLa!r3 » 08 Nov 2006, 18:50
Re,
- a gauche je trouve également

--------------------------------------------------------
-a droite ; - \frac {1}{4})^2)
^2) => Identité remarquable ;
=> Identité remarquable ;(-4)² - 2*(-4)*
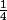
+
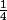
²
16 +

18 +



étant
différent de

,
-2 n'est pas solution.
Tu nous fais la même pour
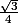
? :we:
lepomédu11 a écrit:Je sens qu'il y a une faute
Moi je dis que tu as du flaire !
Ciao :++:
-
lepomédu11
- Membre Naturel
- Messages: 20
- Enregistré le: 08 Nov 2006, 16:31
-
 par lepomédu11 » 08 Nov 2006, 19:19
par lepomédu11 » 08 Nov 2006, 19:19
Merci claire Tu ma bien aidé sur ce coup
j'avait pas flairé l'identité remarquable
Bon je crois qu'il m'en reste une ^^
-
cLa!r3
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Oct 2006, 22:10
-
 par cLa!r3 » 08 Nov 2006, 19:22
par cLa!r3 » 08 Nov 2006, 19:22
Je ne t'ai pas vraiment aidé, le tip-top aurai été que tu dises ou tu bute exactement, pour qu'on puisse réellement t'aidé à trouvé de toi même.
Fais de même pour
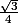
et montre nous ce que tu as fait !
-
lepomédu11
- Membre Naturel
- Messages: 20
- Enregistré le: 08 Nov 2006, 16:31
-
 par lepomédu11 » 08 Nov 2006, 19:54
par lepomédu11 » 08 Nov 2006, 19:54
j'ai trouvé:
A= 10-Racine de 3
B= 13-4Racine de 3
-
cLa!r3
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Oct 2006, 22:10
-
 par cLa!r3 » 08 Nov 2006, 20:24
par cLa!r3 » 08 Nov 2006, 20:24
Bonsoir,
je trouve ;
coté gauche :
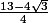
coté droit :
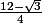
J'ai fais sa vite fait, car la je dois travailler mes cours (donc attend confirmation)
Ciao !
-
lepomédu11
- Membre Naturel
- Messages: 20
- Enregistré le: 08 Nov 2006, 16:31
-
 par lepomédu11 » 08 Nov 2006, 20:27
par lepomédu11 » 08 Nov 2006, 20:27
Tu n'aurais pas le temps de developpé par hasar paske je voit pas ??
-
cLa!r3
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Oct 2006, 22:10
-
 par cLa!r3 » 08 Nov 2006, 20:41
par cLa!r3 » 08 Nov 2006, 20:41
^2 - \frac{\sqrt 3}{4} + \frac{1}{4})
=

=
}{4})
=

A noté : tu peux aussi écrire

comme suis :

----------------------------------------------------------
^2)
Je développe l'id. remarquable ;
^2 - \frac{2\times 2\sqrt 3}{4} \times \frac{1}{4} + (\frac{1}{4})^2)
=

=

A noté : tu peux aussi écrire

comme suis:

(Nota, je m'étais trompé pour le second, j'ai rectifié)
-
cLa!r3
- Membre Relatif
- Messages: 189
- Enregistré le: 18 Oct 2006, 22:10
-
 par cLa!r3 » 08 Nov 2006, 22:42
par cLa!r3 » 08 Nov 2006, 22:42
Re,
as tu compris les développements ?
N'hésite pas !
Ciao
-
lepomédu11
- Membre Naturel
- Messages: 20
- Enregistré le: 08 Nov 2006, 16:31
-
 par lepomédu11 » 09 Nov 2006, 19:16
par lepomédu11 » 09 Nov 2006, 19:16
Salut claire,
J'ai trouve :
13- 4Racine de 3 = 13- 4Racine de 3
Donc Racine de 3/4 est solution
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
