salut!
j'ai plusieurs équations qui me posent problème.
j'ai essayé plusieur de plein de façondifférentes mais je crois que quelque chose m'échappe!
(x+10)/(x-5) + (3-2x)/(x+1) = -1
et
4x²-(x+1)² = 0
merci d avance pour votre aide!je suis dessus depuis 9h du matin,je n en peux plus!! :cry:
équations!
11 messages
- Page 1 sur 1
Bonjour,
Pour ta première équation, réduis tout au même dénominateur, fais passer ce dénominateur de l'autre côté, développe tout et réduis tout. Tu verras apparaître une équation du second degré.
Pour la 2e, tu développes tout et tu vas voir une équation du second degré apparaître.
Bon courage pour les calculs,
Pour ta première équation, réduis tout au même dénominateur, fais passer ce dénominateur de l'autre côté, développe tout et réduis tout. Tu verras apparaître une équation du second degré.
Pour la 2e, tu développes tout et tu vas voir une équation du second degré apparaître.
Bon courage pour les calculs,
pour la première le dénom commun est (x-5)(x+1), tu transposes ensuite -1 à gauche de l'égalité et tu dois résoudre une équation équivalente à la première ds laquelle un quotient s'annulle or tu sais qu'un quotient n'est nul qu'à condition que le numérateur soit nul ... j'te laisse contnuer !
pour la seconde, utilise l'une des trois identités remarquables "de base" pour obtenir l'équation produit équivalente (x-1)(3x+1)=0 que tu sais résoudre assez facilement ! indice : "a^2 - b^2 = ... ici tu travailles avec a=2x et b=x+1 ...
pour la seconde, utilise l'une des trois identités remarquables "de base" pour obtenir l'équation produit équivalente (x-1)(3x+1)=0 que tu sais résoudre assez facilement ! indice : "a^2 - b^2 = ... ici tu travailles avec a=2x et b=x+1 ...
Petit rappel :
a/b + c/d = (ad + cb) / bd
bd est le dénominateur commun.
Dénominateur : Celui des deux nombres exprimant une fraction, qui s'écrit au-dessous de l'autre (source, Dictionnaire de l'Académie Française 1932).
Le dénominateur commun à x-5 et à x+1 est (x-1)(x+5).
Autre rappel (pour la deuxième équation)
a² - b² = (a+b)(a-b)
a/b + c/d = (ad + cb) / bd
bd est le dénominateur commun.
Dénominateur : Celui des deux nombres exprimant une fraction, qui s'écrit au-dessous de l'autre (source, Dictionnaire de l'Académie Française 1932).
Le dénominateur commun à x-5 et à x+1 est (x-1)(x+5).
Autre rappel (pour la deuxième équation)
a² - b² = (a+b)(a-b)
Fraction (niveau seconde)
Bonjour
J'ai un exercice de seconde que je n'arrive pas à résoudre .

L'énoncé est:
Soit la fraction:
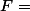

Démontrer que la fraction F est aussi égale à
Pouvez-vous me donner les méthodes ,s'il vous plaît ??
Merci d'avance. :happy:
J'ai un exercice de seconde que je n'arrive pas à résoudre .
L'énoncé est:
Soit la fraction:
Démontrer que la fraction F est aussi égale à
Pouvez-vous me donner les méthodes ,s'il vous plaît ??
Merci d'avance. :happy:
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
