équations et résolution graphique

[lilou0102]

Bonjour,
J'ai un exercice de maths à faire mais je n'arrive pas à le terminer.
Voici l'énoncé :
Peut on trouver trois entiers consécutifs tels que le cube du plus grand soit la somme des cubes des deux autres?
Pour l'instant j'ai mon équation qui est : (x+1)^3 = (x-1)^3 + x^3
Comme je n'ai pas encore fait les équations du troisième degrès, est ce qu'il faut faire une résolution graphique? Et comment trouver ma solution avec ce graphique?
Merci beaucoup

[WillyCagnes]

bjr

tu simplifies ton expression pour trouver f(x)=x^3 -6x² -2
puis tu traces la courbe avec ta calculette ou un tableur connaitre la valeur de x tel que f(x)=0
x= 6,05456....

[lilou0102]

Ok merci!
Mais comment fais-tu pour simplifier l'expression?
Donc si j'ai bien compris il n'y a pas de solution :)

[WillyCagnes]

revoir le developpement de (a+b)^3=?

si tu ne le sais pas alors (a+b)²(a+b) que tu devrais savoir faire

(a²+2ab+b²)(a+b)=?


si il y a une solution mais pas entiere x=6,05456... d'où la résolution graphique utilisée

[lilou0102]

Donc (x+1)^3 = (x+1)^2 * (x+1) ?

[WillyCagnes]

pour developper
(x+1)^3 = (x+1)^2 * (x+1) =(x²+2x+1)(x+1)=? te laisse checher

mais revient à ceci
(x+1)^3 = (x-1)^3 + x^3

x^3 +3x²+3x+1 = [x^3 -3x² +3x-1] +x^3

te laisse simplifier en mettant tous les termes dans le membre de droite ou gauche
f(x)=?

[laetidom]

Bonjour,
J'ai un exercice de maths à faire mais je n'arrive pas à le terminer.
Voici l'énoncé :
Peut on trouver trois entiers consécutifs tels que le cube du plus grand soit la somme des cubes des deux autres?
Pour l'instant j'ai mon équation qui est : (x+1)^3 = (x-1)^3 + x^3
Comme je n'ai pas encore fait les équations du troisième degrès, est ce qu'il faut faire une résolution graphique? Et comment trouver ma solution avec ce graphique?
Merci beaucoup

Bonjour,

traçons (x+1)^3,
traçons (x-1)^3 + x^3

la première courbe (verte) croise ( le = ) la seconde (rouge) en x 6.05456... (et y 351.08...)

graphiquement, la rencontre des deux courbes donne : http://www.cjoint.com/c/FAck3GLKaUf

[lilou0102]

Je trouve bien x^3 - 6x^2 - 2 !
Merci beaucoup pour ton aide !

[lilou0102]

Bonjour,

traçons (x+1)^3,
traçons (x-1)^3 + x^3

la première courbe (verte) croise ( le = ) la seconde (rouge) en x 6.05456... (et y 351.08...)

graphiquement, la rencontre des deux courbes donne : http://www.cjoint.com/c/FAck3GLKaUf

J'avais effectivement tracé mes courbes à l'aide de la fonction graphique de ma calculette, mais comme je ne voyais pas où les courbes se croisaient, je pensais qu'elles ne se croisaient donc pas! Donc il suffit de tracer mes courbes et de dire qu'elles se croisent à 6.054... et donc qu'y a pas de solutions pour les nombres entiers?
En tout cas merci beaucoup pour ton aide!

[laetidom]

J'avais effectivement tracé mes courbes à l'aide de la fonction graphique de ma calculette, mais comme je ne voyais pas où les courbes se croisaient, je pensais qu'elles ne se croisaient donc pas! Donc il suffit de tracer mes courbes et de dire qu'elles se croisent à x = 6.054... et donc qu'y a pas de solutions pour les nombres entiers?
En tout cas merci beaucoup pour ton aide!

lilou,

Effectivement le traceur geogebra permet d'y voir un peu plus clair qu'avec la calculatrice graphique dans ce genre de configuration ! ça te permet rapidement d'aller observer ce qui se passe à une ordonnée de 351... ! et oui la calculatrice peinera dans ce cas là !...

tu peux décrire ce que tu vois sur le graphe...et conclure,

car avec le calcul tu tombe sur x^3-6x²-2 = 0 (http://www.cjoint.com/c/FAclSP8kbQf ) et comme tu ne constate pas de racine évidente entière, tu ne peux pas factoriser ton trinôme et accéder à du second degré plus exploitable...

(le théorème de la valeur intermédiaire te permettrait de trouver une valeur approchée de la racine non entière, mais ça n'est pas l'objet de ton exercice)

Bonne rédaction, bonne journée.

[lilou0102]

Merci!
J'ai tracer mes fonctions sur geogebra avec le tableur, mais je ne trouve pas de point d'intersection, mais sur votre graphique, pourquoi avoir tracé une droite passant par le point B?

[laetidom]

Merci!
J'ai tracer mes fonctions sur geogebra avec le tableur, mais je ne trouve pas de point d'intersection, mais sur votre graphique, pourquoi avoir tracé une droite passant par le point B?

pour te montrer que cette droite est à la verticale du point d'intersection des 2 courbes !

ma courbe verte et ma courbe rouge ne sont pas parallèles, elles tendent l'une vers l'autre et se croisent à " l'altitude " 351...

[Ben314]

Salut,
Juste une remarque pour signaler que, lorsque l'on cherche à résoudre des équations Diophantiennes (c'est à dire des équations dont on cherche les solutions entières), on utilise très souvent la notion de divisibilité des nombres entiers plutôt que des études de fonctions.
Par exemple, ici peut s'écrire .
Dans R une telle écriture de la forme AxB=2 est sans intérêt vu qu'on peut prendre n'importe quoi (de non nul) pour A puis prendre B=2/A (c'est pour cette raison que dans R, on se ramène systématiquement à des équation de la forme AxB=0).
Mais, avec les entiers, c'est totalement différent vu que le nombre 2 n'a qu'un nombre fini de diviseurs entiers, à savoir -2,-1,1 et 2.
Donc, pour que , il faut que 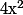soit égal à -2,-1,1 ou 2.
Clairement, seule la valeur 1 est possible (avec x entier) ce qui correspond à x=1 ou -1. Sauf que ça ne marche pas ni dans un cas, ni dans l'autre...

[laetidom]

Salut,
Juste une remarque pour signaler que, lorsque l'on cherche à résoudre des équations Diophantiennes (c'est à dire des équations dont on cherche les solutions entires), on utilise très souvent la notion de divisibilité des nombres entiers plutôt que des études de fonctions.
Par exemple, ici peut s'écrire .
Dans R une telle écriture de la forme AxB=2 est sans intérêt vu qu'on peut prendre n'importe quoi (de non nul) pour A puis prendre B=2/A (c'est pour cette raison que dans R, on se ramène systématiquement à des équation de la forme AxB=0).
Mais, avec les entiers, c'est totalement différent vu que le nombre 2 n'a qu'un nombre fini de diviseurs entiers, à savoir -2,-1,1 et 2.
Donc, pour que , il faut que soit égal à -2,-1,1 ou 2.
Clairement, seule la valeur 1 est possible (avec x entier) ce qui correspond à x=1 ou -1. Sauf que ça ne marche pas ni dans un cas, ni dans l'autre...

Très clair Ben !, merci pour l'info.

[lilou0102]

Merci à tous pour vos réponses!