Equations et pourcentages - Mise à Niveau
42 messages
- Page 1 sur 3 - 1, 2, 3
Equations et pourcentages - Mise à Niveau
Bonjour,
Je m'arrache les cheveux depuis une heure et demie sur un problème dont j'ai le corrigé (autocorrection avec le CNED), mais je n'arrive pas à comprendre celui-ci :
"Un commerçant accorde à ses clients, sur les prix marqués, deux escomptes successifs de x% et 2x. Calculer x et 2x sachant que le pourcentage du rabais total ainsi consenti est de 15%."
J'ai compris ce qu'il faut faire mais je ne sais pas du tout comment faire, et j'ai beau lire et relire le corrigé je ne comprends toujours pas. Ca fait partie du cours sur les équations.
J'ai beaucoup de lacunes en mathématiques (j'ai peu de souvenirs sur le calcul de pourcentages).
Merci à ceux et/ou celles qui m'aideront
Je m'arrache les cheveux depuis une heure et demie sur un problème dont j'ai le corrigé (autocorrection avec le CNED), mais je n'arrive pas à comprendre celui-ci :
"Un commerçant accorde à ses clients, sur les prix marqués, deux escomptes successifs de x% et 2x. Calculer x et 2x sachant que le pourcentage du rabais total ainsi consenti est de 15%."
J'ai compris ce qu'il faut faire mais je ne sais pas du tout comment faire, et j'ai beau lire et relire le corrigé je ne comprends toujours pas. Ca fait partie du cours sur les équations.
J'ai beaucoup de lacunes en mathématiques (j'ai peu de souvenirs sur le calcul de pourcentages).
Merci à ceux et/ou celles qui m'aideront
bjr
x en pourcentage
1ère ristourne= prix.(x)
donc le nouveau prix2= prix -prix.(x)=prix (1-x)
2è ristoune = prix2.(2x)
donc le nouveau prix3 = prix2 -prix2.(2x)= prix2(1-2x)
et au final je remplace prix2 par le prix(1-x)
prix3= prix(1-x)(1-2x)
prix3 = prix -0,15prix = prix (1-x)(1-2x)
soit 1-0,15= (1-x)(1-2x) à resoudre
x en pourcentage
1ère ristourne= prix.(x)
donc le nouveau prix2= prix -prix.(x)=prix (1-x)
2è ristoune = prix2.(2x)
donc le nouveau prix3 = prix2 -prix2.(2x)= prix2(1-2x)
et au final je remplace prix2 par le prix(1-x)
prix3= prix(1-x)(1-2x)
prix3 = prix -0,15prix = prix (1-x)(1-2x)
soit 1-0,15= (1-x)(1-2x) à resoudre
Thib' a écrit:On posele prix de départ.
Par hypothèse on a :.
Il ne te reste plus qu'à résoudre l'équation. Tu comprends mieux ?
Non je ne comprends pas, peut-être parce que ça fait des heures que j'ai le nez dedans, en tout cas mon corrigé est beaucoup plus compliqué : déjà le correcteur choisit 100 comme prix de départ ("par commodité" dit-il, on peut faire ça ?), ensuite il détermine que :
Le prix après le premier escompte est 100-x
Le deuxième escompte est de 2x % et donc d'un montant de
Donc le prix net est de
Ensuite il simplifie cette fraction jusqu'à
WillyCagnes a écrit:bjr
x en pourcentage
1ère ristourne= prix.(x)
donc le nouveau prix2= prix -prix.(x)=prix (1-x)
2è ristoune = prix2.(2x)
donc le nouveau prix3 = prix2 -prix2.(2x)= prix2(1-2x)
et au final je remplace prix2 par le prix(1-x)
prix3= prix(1-x)(1-2x)
prix3 = prix -0,15prix = prix (1-x)(1-2x)
soit 1-0,15= (1-x)(1-2x) à resoudre
C'est plus clair mais ça n'a rien à voir avec mon corrigé. Je vais le réecrire ce sera plus simple si quelqu'un peut le commenter.
Pas grave Thib !
Voici le corrigé exact :
"Les escomptes sont indiqués en pourcentage, il est commode de considérer un prix marqué de 100 euros.
Le premier escompte est donc de et le prix après cet escompte est
et le prix après cet escompte est  .
.
Le deuxième escompte étant de , son montant est de
, son montant est de  \times \frac {2x}{100}) .
.
Ainsi le prix net est :
-(100 - x) \frac {2x}{100} = \frac {(100-x)100}{100} - (100 - x) \frac {2x}{100} = \frac {(100-x)(100-2x)}{100}) .
.
or le prix net pour un rabais de 15% sur 100 euros est égal à 85 euros.
On doit donc avoir(100-2x)}{100} = 85) soit
soit (100-2x) = 8500)
En développant on obtient : soit
soit  ou encore
ou encore  en simplifiant par 2.
en simplifiant par 2.
Cette équation est une équation polynomiale du second degré dont le domaine de définition est .
.
Calculons le discriminant :
: ^2 - 4 \times 1 \times 750 = 19500) .
.
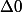 donc l'équation admet deux solutions
donc l'équation admet deux solutions  et
et  définies par :
définies par :
 et
et 
le bon sens exige que la solution soit écartée car l'inconnue est un pourcentage et donc ne peut excéder 100.
soit écartée car l'inconnue est un pourcentage et donc ne peut excéder 100.
En conclusion, et
et  . (
. ( )"
)"
Voilà voilà ! Autant vous dire que j'ai rien compris dès la première phrase. Première question : dans quels cas on a le droit de remplacer des chiffres comme ça, "par commodité", est-ce que ça se fait souvent ?
EDIT : J'ai complété le corrigé et rajouté ma question à la fin.
"Les escomptes sont indiqués en pourcentage, il est commode de considérer un prix marqué de 100 euros.
Le premier escompte est donc de
Le deuxième escompte étant de
Ainsi le prix net est :
or le prix net pour un rabais de 15% sur 100 euros est égal à 85 euros.
On doit donc avoir
En développant on obtient :
Cette équation est une équation polynomiale du second degré dont le domaine de définition est
Calculons le discriminant
le bon sens exige que la solution
En conclusion,
Voilà voilà ! Autant vous dire que j'ai rien compris dès la première phrase. Première question : dans quels cas on a le droit de remplacer des chiffres comme ça, "par commodité", est-ce que ça se fait souvent ?
EDIT : J'ai complété le corrigé et rajouté ma question à la fin.
Leotard a écrit:Non je ne comprends pas, peut-être parce que ça fait des heures que j'ai le nez dedans, en tout cas mon corrigé est beaucoup plus compliqué : déjà le correcteur choisit 100 comme prix de départ ("par commodité" dit-il, on peut faire ça ?), ensuite il détermine que :
Le prix après le premier escompte est 100-x
Le deuxième escompte est de 2x % et donc d'un montant dex
Donc le prix net est de
Ensuite il simplifie cette fraction jusqu'à= 85 mais le corrigé est encore long. Vu que je me base sur leur guide ce serait peut-être mieux pour moi de suivre leur méthode, qu'en pensez-vous ?
100 n'est pas un prix, on part du principe que
Leotard a écrit:C'est pourtant ce qu'écrit le correcteur, mais c'est vrai que je ne comprends pas comment cela se fait.
C'est un peu tiré par les cheveux mais bon, en sachant que le prix de base est 100, la suite est facile à mettre en oeuvre sauf un detail, il n'exprime pas x en pourcentage ce qui me surprend .
Shew a écrit:C'est un peu tiré par les cheveux mais bon, en sachant que le prix de base est 100, la suite est facile à mettre en oeuvre sauf un detail, il n'exprime pas x en pourcentage ce qui me surprend .
Justement je me demandais pourquoi 2x% mais x tout court.
Sinon tu comprends tout le calcul alors ?
Leotard a écrit:Justement je me demandais pourquoi 2x% mais x tout court.
Sinon tu comprends tout le calcul alors ?
Oui le calcul est facile on ramène tout au même dénominateur et (100 - x) est un facteur commun
donc on peut écrire
Shew a écrit:Oui le calcul est facile on ramène tout au même dénominateur et (100 - x) est un facteur commun
donc on peut écrire. Comme
, on multiplie par 100 des deux côtés ainsi on est plus importuné par le dénominateur . Developper
peut s'averer toutefois contraignant puisqu'il s'agit de grands nombres mais passe ce point on se retrouve avec une trinome du second degrés que l'on simplifie et que l'on traite facilement si on connait bien les formules :lol3: .
Dit comme ça ca a l'air beaucoup plus simple, je vais réessayer. Merci !
Leotard a écrit:J'ai un souci. Je comprends comment on passe deà
100}{100} - (100 - x) \frac {2x}{100})
,mais pas deà
J'ai compris pour le facteur commun mais si j'avais eu à l'appliquer j'aurais fait un gros n'importe quoi genre, bref je n'ai pas encore bien compris la règle. Une explication ?
Il faut factoriser puisque (100 - x) est un terme que l'on retrouve deux fois dans l'expression :
On peut ecrire
Shew a écrit:Il faut factoriser puisque (100 - x) est un terme que l'on retrouve deux fois dans l'expression :
On peut ecrirecomme ceci
Ok je crois que je commence à comprendre : j'étais perturbé à cause des parenthèses autour de 100 et 2x, mais c'est normal qu'elles soient là du coup sinon le (100-x) ne se multiplie qu'avec le premier nombre !
(pfiou une demi heure pour comprendre ça :euh: )
Bon, je continue. Merci une fois de plus Shew !
Une énième question, jusque là j'ai appris comment factoriser, comment développer mais concrètement à quoi ça me sert pour résoudre des équations ? Je sais que pour résoudre une équation il faut qu'elle soit à un certain "format" genre 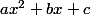 mais comment je sais à quel moment développer, à quel moment factoriser ?
mais comment je sais à quel moment développer, à quel moment factoriser ?
Est-ce que c'est pour pouvoir simplifier au maximum les expressions, genre "j'ai un produit de facteurs irréductible, je le développe et sous forme développée je ne peux plus le réduire, donc je refactorise et je peux le réduire encore plus etc..." et dans ce cas comment on sait qu'on peut arrêter les transformations ?
Est-ce que c'est pour pouvoir simplifier au maximum les expressions, genre "j'ai un produit de facteurs irréductible, je le développe et sous forme développée je ne peux plus le réduire, donc je refactorise et je peux le réduire encore plus etc..." et dans ce cas comment on sait qu'on peut arrêter les transformations ?
Leotard a écrit:Une énième question, jusque là j'ai appris comment factoriser, comment développer mais concrètement à quoi ça me sert pour résoudre des équations ? Je sais que pour résoudre une équation il faut qu'elle soit à un certain "format" genremais comment je sais à quel moment développer, à quel moment factoriser ?
Est-ce que c'est pour pouvoir simplifier au maximum les expressions, genre "j'ai un produit de facteurs irréductible, je le développe et sous forme développée je ne peux plus le réduire, donc je refactorise et je peux le réduire encore plus etc..." et dans ce cas comment on sait qu'on peut arrêter les transformations ?
On developpe généralement sur demande ou lorsque l'equation implique une égalité differente de zero : Ex:
Shew a écrit:On developpe généralement sur demande ou lorsque l'equation implique une égalité differente de zero : Ex:. A l'inverse on factorise lorsque l'egalité est à zero mais comme vous devez le savoir des fois on ne peut pas factoriser alors on utilise le discriminant et la formule de resolution des trinomes du second degrés . Factoriser permet d'identifier certains termes, de mettre en evidence des formes que l'on connait .
J'ajoute tout de suite cette réponse à mes notes personnelles ! (étonnamment ça n'est pas dans le support de cours)
J'arrive à la partie de l'exercice sur les équations polynomiales donc je pense que j'ai bien tout compris le reste. Merci mille fois Shew !
Une dernière question (pour de vrai), le corrigé dit "l'inconnue est un pourcentage et donc ne peut excéder 100", c'est forcément vrai ? Je ne connaissais pas cette règle.
Leotard a écrit:J'ajoute tout de suite cette réponse à mes notes personnelles ! (étonnamment ça n'est pas dans le support de cours)
J'arrive à la partie de l'exercice sur les équations polynomiales donc je pense que j'ai bien tout compris le reste. Merci mille fois Shew !
Une dernière question (pour de vrai), le corrigé dit "l'inconnue est un pourcentage et donc ne peut excéder 100", c'est forcément vrai ? Je ne connaissais pas cette règle.
Tout depend de l'exercice, on peut se retrouver avec une part d'augmentation supèrieur à 100 .
42 messages
- Page 1 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 102 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
