Equations de plans et de droites

[Antoine1998]

Bonjour

Comment fait on pour savoir si le vecteur directeur fait parti du plan ( ex c) . Idem pour un point, s il fait partie du plan ( ex b)

[mathelot]

bonjour,
pour savoir si un point M(u;v;w) appartient au plan (P)
on remplace (x;y;z) par (u;v;w) , si on obtient une égalité vraie, c'est que le point M appartient au plan
sinon M n'appartient pas au plan.
pour la (c) un vecteurest dans la direction de P,ie, appartient à si et seulement si il est orthogonal à un vecteur normal non nul.

[capitaine nuggets]

Salut !

- Pour la question a) :

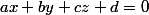
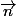
Théorème important : Soit un plan d'équation cartésienne , avec non tous nuls. Alors un vecteur normal de ce plan est .

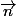
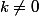
Remarque : Comme tout vecteur colinéaire à est aussi normal à , on en déduit qu'en fait tous les vecteurs , avec , sont normaux à .

Et tu as aussi la réciproque.

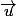
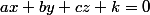
Réciproque du théorème : Soit un vecteur de coordonnées . Alors tout plan d'équation cartésienne , avec réel quelconque, est un plan normal à .

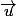
- Pour la question b) :

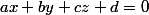
Un point de coordonnées appartient à un plan d'équation cartésienne , si et seulement si les coordonnées de vérifient l'équation de , c'est-à-dire si et seulement si on a .

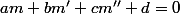
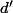
- Pour la question c) : il y a un problème : ça n'a pas de sens de parler de vecteur directeur pour un plan. L'usage veut qu'on en parle pour une droite dans le but d'en donner la direction, mais pour un plan ça n'est pas possible puisque par une droite passe une infinité de plans ! 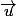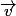Néanmoins, la connaissance de deux droites et sécantes permet de déterminer entièrement le plan contenant ces deux droites, donc on pourrait donner deux vecteurs : un vecteur directeur de et un vecteur directeur de . 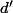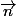Pour remédier à cela, on a introduit la notion de vecteur normal (qui fait la liaison entre les deux vecteurs directeur et le vecteur normal via le produit vectoriel).

[mathelot]

pour la (c) , le plan vectoriel qui dirige le plan affine (P) est noté
Deux vecteurs, non liés, de donnent la direction de (P)

[Antoine1998]

D'accord j'ai compris. Merci