Equations paramétriques

[fodediarra11s]

Excercice
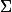
On considère le système ( ) suivant dans lequel m est un paramètre réel :

(x,y)
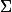
1) Résoudre ( ) pour m=0
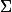
2)Il y'a deux valeurs de m pour lesquels ( ) admet une solution unique.Déterminer ces deux réels.On pourra d'abord résoudre le système extrait
.
3) Pour chaque valeur de m trouvée dans la 2),donner la solution unique correspondante du système ( )

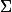
[Dinozzo13]

Utilise la méthode des déterminants.

[fodediarra11s]

Utilise la méthode des déterminants.

je suis passé par cette méthode et X=Dx/D et Y=Dy/D ensuite comme on a dit deux solutions identiques donc j'ai poser X=Y mais j'arrive po à trouver les valeurs de m

[Dinozzo13]

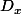
Le système admet une unique solution, où désigne le déterminant du système et , les déterminants relatifs à et , si et seulement si .

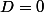
Si alors soit il n'y aucune solutions, soit une infinité.

Mais je comprends pas ce que tu veux savoir : ton exercice parle de solution unique.