équations factorielles
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
apachetransfire
- Membre Naturel
- Messages: 66
- Enregistré le: 26 Oct 2013, 19:11
-
 par apachetransfire » 20 Avr 2015, 18:03
par apachetransfire » 20 Avr 2015, 18:03
Bonjour à tous ;
je suis un peu curieux alors voila :
existe t-il une méthode concrète afin de résoudre une équation du type
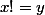
dans N
ou au moins de savoir s'il existe une solution.... je sais qu'un factoriel est toujours pair sinon c'est tout..
:mur:

-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 20 Avr 2015, 18:42
par capitaine nuggets » 20 Avr 2015, 18:42
apachetransfire a écrit:Bonjour à tous ;
je suis un peu curieux alors voila :
existe t-il une méthode concrète afin de résoudre une équation du type
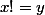
dans N
ou au moins de savoir s'il existe une solution.... je sais qu'un factoriel est toujours pair sinon c'est tout..
:mur:
Salut !
La factorielle n'est déjà définie que sur l'ensemble des entiers naturels.
Ensuite, il faut savoir que pour

,

est égal au produit des

premiers entiers de

jusqu'à

(avec comme convention
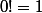
), donc ça augmente très vite.
Les premières valeurs de

, sont :

etc...
Donc par exemple l'équation d'inconnue

,
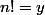
où

appartient à

n'admet aucune solution.
-
apachetransfire
- Membre Naturel
- Messages: 66
- Enregistré le: 26 Oct 2013, 19:11
-
 par apachetransfire » 20 Avr 2015, 19:15
par apachetransfire » 20 Avr 2015, 19:15
capitaine nuggets a écrit:Salut !
La factorielle n'est déjà définie que sur l'ensemble des entiers naturels.
Ensuite, il faut savoir que pour

,

est égal au produit des

premiers entiers de

jusqu'à

(avec comme convention
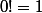
), donc ça augmente très vite.
Les premières valeurs de

, sont :

etc...
Donc par exemple l'équation d'inconnue

,
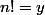
où

appartient à

n'admet aucune solution.
Merci pour tes informations ! , mais sur un intervalle plus grand , disons [0,100000] , n'y aurait t-il
pas d'autres critères discriminants ( autre que la parité ) pour savoir si selon y appartenant a N ,
x! n'aurait pas de solution avec x appartenant à N ; au lieu de les apprendre par coeur .
je m'intéresse actuellement au problème de brocard ; et donc un pas de plus dans le domaine
des factorielles ne serait pas de refus


-
capitaine nuggets
- Modérateur
- Messages: 3931
- Enregistré le: 13 Juil 2012, 22:57
- Localisation: nulle part presque partout
-
 par capitaine nuggets » 20 Avr 2015, 19:23
par capitaine nuggets » 20 Avr 2015, 19:23
apachetransfire a écrit: capitaine nuggets a écrit:Salut !
La factorielle n'est déjà définie que sur l'ensemble des entiers naturels.
Ensuite, il faut savoir que pour

,

est égal au produit des

premiers entiers de

jusqu'à

(avec comme convention
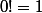
), donc ça augmente très vite.
Les premières valeurs de

, sont :

etc...
Donc par exemple l'équation d'inconnue

,
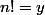
où

appartient à

n'admet aucune solution.
Merci pour tes informations ! , mais sur un intervalle plus grand , disons [0,100000] , n'y aurait t-il
pas d'autres critères discriminants ( autre que la parité ) pour savoir si selon y appartenant a N ,
x! n'aurait pas de solution avec x appartenant à N ; au lieu de les apprendre par coeur .
je m'intéresse actuellement au problème de brocard ; et donc un pas de plus dans le domaine
des factorielles ne serait pas de refus

On peut avoir des renseignements supplémentaires pour des nombres, très grands.
Par définition
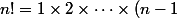\times n)
donc pour
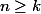
,

est un multiple de

,

est un multiple de

,

est un multiple de

, ... ,

est un multiple de
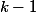
,

est un multiple de

.
Du coup, par exemple, 4!, 5!, 6!, 7! sont au moins multiples de 2, 3 et 4.
Mais de toute façon la factorielle croit très rapidement donc pour n entier compris entre 1 000 et 100 000, il n'existe pas beaucoup d'entiers y tels que n!=y
:+++:
-
apachetransfire
- Membre Naturel
- Messages: 66
- Enregistré le: 26 Oct 2013, 19:11
-
 par apachetransfire » 20 Avr 2015, 19:39
par apachetransfire » 20 Avr 2015, 19:39
Dans le cadre du problème de brocard qui stipule l'équivalence
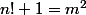
si la représentation de
=x!+1)
était en théorie possible sur N ; il suffirait
de représenter la fonction carrée sur N ; puis de démontrer qu'il n'existe pas ; au delà
d'un certain seuil ; qu'il n'existe pas de droites d'équation y=k qui coupent les deux
fonctions ....... à mon avis on s'est ramené à un problème plus complexe là :ptdr:
mais cela est impossible a mon avis
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
dans N
,
est égal au produit des
premiers entiers de
jusqu'à
(avec comme convention
), donc ça augmente très vite.
, sont :
etc...
,
où
appartient à
n'admet aucune solution.
,
est égal au produit des
premiers entiers de
jusqu'à
(avec comme convention
), donc ça augmente très vite.
, sont :
etc...
,
où
appartient à
n'admet aucune solution.