Equations cyclométriques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 17 Oct 2021, 21:43
par Lucie22 » 17 Oct 2021, 21:43
Bonjour à tous!
Pouvez-vous m'aider à résoudre cet exercice?
Résous dans ℝ:
+Arccos\frac{1}{x}=Arcsin\frac{x}{x-2})
Merci d'avance!

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 17 Oct 2021, 23:07
par Ben314 » 17 Oct 2021, 23:07
Salut,
C'est quoi le domaine de définition de ton équation ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 06:42
par Lucie22 » 18 Oct 2021, 06:42
Salut! Merci pour ta réponse! Je dois définir le domaine moi-même

-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 18 Oct 2021, 06:50
par Pisigma » 18 Oct 2021, 06:50
Bonjour,
Lucie22 a écrit:Salut! Merci pour ta réponse! Je dois définir le domaine moi-même

ben oui, évidemment!
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 17:14
par Lucie22 » 18 Oct 2021, 17:14
J'ai trouvé domf = ] 0;2 [
Mais pouvez-vous m'aider pour la suite, je n'y arrive pas?
Merci d'avance !

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Oct 2021, 17:18
par Ben314 » 18 Oct 2021, 17:18
Ce n'est pas ce que j'ai trouvé (et ce que j'ai trouvé aide beaucoup pour la suite . . .)
Détaille tes calculs pour que l'on te dise où est située ton erreur (ou la mienne . . .)
Rappel : Les fonctions Arcsin et Arccos sont toutes les deux définies sur l'intervalle fermé [-1,1]
De plus, la première est à valeur dans [-pi/2;pi/2] et la seconde dans [0,pi] (faire un cercle trigo pour le retrouver) mais ce n'est pas utile pour évaluer le domaine de définition de l'équation
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 17:36
par Lucie22 » 18 Oct 2021, 17:36
Voilà ce que j'ai trouvé:
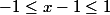
donc
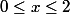
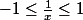
donc
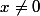
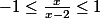
donc
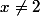
-
mathelot
 par mathelot » 18 Oct 2021, 20:04
par mathelot » 18 Oct 2021, 20:04
Lucie22 a écrit:Voilà ce que j'ai trouvé:
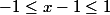
donc
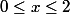 (1)
(1)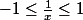
donc
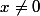 (2)
(2)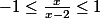
donc
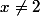 (3)
(3)
De (1) on tire
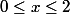
de (2)
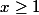
d'où
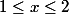
il reste à exploiter les inéquations (3)
en dressant le tableau de variations de f, f(x)=x/(x-2)
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 20:19
par Lucie22 » 18 Oct 2021, 20:19
Ok, merci beaucoup !
Après avoir défini le domaine que dois-je faire? Dois-je utiliser la formule sin (a+b)= sina.cosb + sinb.cosa pour résoudre l'équation?
Merci pour ton aide !
-
mathelot
 par mathelot » 18 Oct 2021, 20:29
par mathelot » 18 Oct 2021, 20:29
Lucie22 a écrit:Dois-je utiliser la formule sin (a+b)= sina.cosb + sinb.cosa pour résoudre l'équation?
il faut absolument préciser le domaine de définition de l'équation. fais l'étude de fonction de f, f(x)=x/(x-2)
avant de commencer la résolution
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 21:01
par Lucie22 » 18 Oct 2021, 21:01
J'ai obtenu [tex]x\leq 1[\tex]. Est-ce juste?
-
mathelot
 par mathelot » 18 Oct 2021, 21:03
par mathelot » 18 Oct 2021, 21:03
oui, c'est ok.
quel est le domaine finalement ?
-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 21:04
par Lucie22 » 18 Oct 2021, 21:04
Super, merci ! 1?
-
mathelot
 par mathelot » 18 Oct 2021, 21:14
par mathelot » 18 Oct 2021, 21:14
oui.
l'équation a t elle des solutions ?
heureusement que l'on résout l'équation de cette manière car sinon, avec la formule sin(a+b)
on obtient une équation polynomiale de degré 6

-
Lucie22
- Membre Naturel
- Messages: 14
- Enregistré le: 17 Oct 2021, 20:19
-
 par Lucie22 » 18 Oct 2021, 21:23
par Lucie22 » 18 Oct 2021, 21:23
Non, l'équation n'a pas de solution car quand on remplace les x par 1 dans l'équation, on obtient 0 = -pi/2. C'est bien ça?
Oui, effectivement, je n'aurai jamais réussi à la résoudre. Merci beaucoup pour ton aide!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
donc
(1)
donc
(2)
donc
(3)