Equations x²+x+k=0 comment toutes les résoudres
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Lip
- Messages: 9
- Enregistré le: 29 Mai 2006, 14:54
-
 par Lip » 30 Mai 2006, 08:20
par Lip » 30 Mai 2006, 08:20
Secondes :
Voici une méthode pour résoudre toues les équations du second dégrés :id:
Elle est infaillible et rapide (pas besoin de factoriser) :zen:
Prenons un exemple numérique :X²+5X+4=0
On considère que le coefficient de X² est A, celui de X est B, et que 4 est C.
On calcule DELTA = B²-4(AC)=5²-4(1*4)=25-16=9Ensuite SI :  DELTA est positif l'équation a deux solutions
DELTA est positif l'équation a deux solutions
X= ( -B+;)DELTA)/2A
X'= ( -B++;)DELTA)/2A  Delta est négatif dans ce cas l'équations n'a pas de solutions
Delta est négatif dans ce cas l'équations n'a pas de solutions  Delta est nul dans ce cas l'équation a une seule solution (-B)/2A
Delta est nul dans ce cas l'équation a une seule solution (-B)/2AViolà donc pour notre équation sa donne :
X=-1
X'=-4
:briques: :briques: :briques: :briques: :briques: :briques: :briques: :briques:
-
bernie
- Membre Relatif
- Messages: 343
- Enregistré le: 01 Mai 2005, 01:14
-
 par bernie » 30 Mai 2006, 10:26
par bernie » 30 Mai 2006, 10:26
Bonjour,
c'est ce que l'on voit en 1ère et qu'il est interdit d'utiliser en seconde sauf au brouillon, à titre de vérification.
A+
 par Daragon geoffrey » 30 Mai 2006, 11:01
par Daragon geoffrey » 30 Mai 2006, 11:01
slt plus simplement il existe une méthode un peu plus complexe (quoique), et qui est la suivante : à partir de x^2 + x + k, avec k un réel qcq, on fait apparaître une identité remarquable : soit (x+1/2)^2 + k - 1/4 =0 équiv à
(x+1/2)^2 = (1/4)-k donc cette équation admet une sdolution ssi (1/4)-k poositif équiv à k inf (ou égal) à 1/4 ! je pense que c'est plus du niveau de seconde ! @ +
-
Tqup3
- Membre Naturel
- Messages: 74
- Enregistré le: 27 Mai 2006, 20:22
-
 par Tqup3 » 30 Mai 2006, 16:17
par Tqup3 » 30 Mai 2006, 16:17
Oui et puis il faut préciser que pour le delta négatif, le polynôme admet des racines dans C.
Exemple: delta = -4 = (iV4)²
A ce moment là, les solutions sont de la même forme que pour le delta positif :)
PS: V = racine carrée
Tqup3
-
Lip
- Messages: 9
- Enregistré le: 29 Mai 2006, 14:54
-
 par Lip » 30 Mai 2006, 16:18
par Lip » 30 Mai 2006, 16:18
Je parlais de vérification bien sûr pas de rédaction !!!!!!
-
allomomo
- Membre Irrationnel
- Messages: 1231
- Enregistré le: 01 Mai 2005, 01:14
-
 par allomomo » 30 Mai 2006, 20:37
par allomomo » 30 Mai 2006, 20:37
Salut,
C'est une méthode très connue ...

Pour n=2
-Si
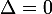
: Il y a une seul solution
-Si

: Il y a deux solutions
-Si

: Il n y a pas de solutions mais il y a n solutions dans dans C.
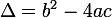
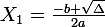
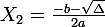
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
