Equations ccontenant des racines carrées

[omryomar2]

Je ne sais pas comment résoudre ces équations :
Racine(2x+2)=(racine(x+1)) + 2

[Sake]

Je ne sais pas comment résoudre ces équations :
Racine(2x+2)=(racine(x+1)) + 2

Salut,

sqrt(2x + 2) = sqrt(2)*sqrt(x + 1)

[laetidom]

Je ne sais pas comment résoudre ces équations :
Racine(2x+2)=(racine(x+1)) + 2

Bjr,

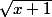
= + 2

Condition : x -1

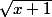
()² = ( + 2)²

[Sake]

Bjr,

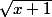
= + 2

Condition : x -1

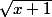
()² = ( + 2)²

On peut trouver plus facile.

[omryomar2]

Merci à vous tous
je ne sais pas comment continuer.
J'ai trouvé :
x-3=2*sqrt(x+1)

[Sake]

Merci à vous tous
je ne sais pas comment continuer.

Pour x 1,

sqrt(2x + 2)=sqrt(x + 1) + 2

c-à-d :

(sqrt(2) - 1)sqrt(x + 1) = 2

i.e. :

sqrt(x + 1) = 2/(sqrt(2) - 1)

ce qui implique que...

[omryomar2]

ce qui implique : x=11+8*sqrt(2)
est-ce exact.
merci

[Sake]

ce qui implique : x=11+8*sqrt(2)
est-ce exact.
merci

???

En partant de sqrt(x + 1) = 2/(sqrt(2) - 1), on prend le carré :

|x + 1| = 4/(sqrt(2) - 1)²

Or x 1 donc |x + 1| = x + 1, d'où :

x = 4/(sqrt(2) - 1)² - 1

Moi je trouve plutôt que , sauf erreur.

[omryomar2]

sqrt(x+1) est défini pour x>=-1, dans ce cas sqrt²(x+1)=x+1
et aussi abs(x+1), x+1>0 ssi x>=-1

[Sake]

sqrt(x+1) est défini pour x>=-1, dans ce cas sqrt²(x+1)=x+1
et aussi abs(x+1), x+1>0 ssi x>=-1

Oui, -1 pardon, j'avais oublié le signe "moins". Par contre, ce que tu racontes est incompréhensible, Omar.

[omryomar2]

voici comment j'ai fais !
;)(x+1)= 2/(;)(2 )-1)=2(;)2+1)
x+1=4(;)2+1)^2
x=12+8;)2-1
x=11+8;)2

[Sake]

voici comment j'ai fais !
(x+1)= 2/(;)(2 )-1)=2(;)2+1)
x+1=4(;)2+1)^2
x=12+8;)2-1
x=11+8;)2

Oui en fait on trouve la même chose.

[omryomar2]

Merci
Je veux savoir comment écrire les symboles mathématiques.

[mathelot]

Merci
Je veux savoir comment écrire les symboles mathématiques.

racine
[.TEX]\sqrt{a}[/TEX]
quotient
[.TEX]\frac{a}{b}[/TEX]
puissance
[.TEX]a^b[/TEX]

[omryomar2]

Et pour cette équation comment faire !
sqrt(2x+1)=sqrt(x+1)+2

[biss]

Et pour cette équation comment faire !
sqrt(2x+1)=sqrt(x+1)+2

si tu sais resoudre des equation du second degrer a une inconnu ta qu'a devellopper

[mathelot]

Et pour cette équation comment faire !
\sqrt{2x+1}=\sqrt{x+1}+2

à écrire entre balises TEX

[omryomar2]

Résoudre dans IR :

[omryomar2]

Merci mathelot

[omryomar2]

Donne moi une astuce pour résoudre cette équation stp