équations cartésiennes

[mariesa]

Bonjour,
J'ai fait un exercice en classe qui me semblait juste mais ma professeur m'a dit que le résultat était faux et m'a donné le résultat sans me montrer la démarche. Je suis dessus depuis 1h mais je n'arrive pas à parvenir au bon résultat.

l'énoncé: Trouver la droite cartésienne de la droite (d).
(d) passe par A(7/4;8/5) et est parallèle à la droite (f) d'équation 4/5x -5/7y +3/8 = 0

J'ai fait: (il n'y a normalement pas de parenthèses mais j'étais obligée de les mettre car sinon ça faisait des smileys)
4/5 x xA -5/7 x yA +c = 0
4/5 x 7/4 + (-5/7) x (8/5) +c = 0
7/5 + (-8/7) +c = 0
35/25 - 40/25+c = 0
-5/25 +c = 0
-1/5 +c = 0
c=1/5

Donc 4/5x-5/7y+1/5=0 est une équation cartésienne de (d).

Mais ma prof a trouvé:
4/5x - 5/7 y - 9/20 = 0 soit 28x - 25y - 9 = 0

Pouvez vous me mettre sur la piste?

[Ben314]

Salut,
(1) 25 n'est pas un dénominateur commun à 7 / 5 et 8 / 7.
(2) 8 / 7 c'est pas franchement égal à 40 / 25....

[anthony_unac]

J'ai fait:
4/5 x xA -5/7 x yA +c = 0
4/5 x 7/4 + (-5/7) x (8/5) +c = 0

Bonsoir,
Avez vous essayé de mettre directement 4/5 en facteur (sachant que 8 /5=2*4/5) ?

[laetidom]

" . . . je n'arrive pas à parvenir au bon résultat. "



Bonjour,

Petite visualisation :

116.JPG (18.92 Kio) Vu 272 fois

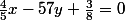(f) : donne 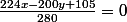et donc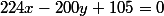

(f) et (d) sont // donc de même vecteur directeur " ( - b ; a ) " soit (200 ; 224) d'où :

(d) :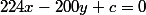 tout en sachant que (d) passe par A donc les coordonnées de A vérifient l'équation de (d) ce qui donne :

=====>

==>

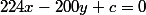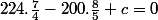
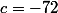
Donc (d) :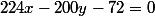 , multiplions de chaque côté de l'égalité par 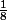ce qui donne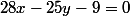


_________________________________
(f) :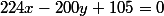
(d) :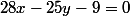
_________________________________

Bonne journée @ tous.