Bonjour à tous . euh dans cet exercice il est dit de résoudre l'équation suivante:
x^4-2(a²+b²)x²+(a²-b² )²=0
J'ai fait un changement de variable en posant X=x² donc on a X²-2(a²+b² )X+(a²-b² ).. Arrivé la je suis bloqué a cause des réel a et b .
équations bicarrées
12 messages
- Page 1 sur 1
Re: équations bicarrées
salut
donc en gros tu n'as rien ...
x^2 + (a^2 - b^2)^2 = [x^2 - (a^2 + b^2)]^2 + (a^2 - b^2)^2 - (a^2 + b^2)^2 = ...)
donc en gros tu n'as rien ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: équations bicarrées
Salut !
Que vaut le discriminant ?
?
(Il va y avoir des simplifications)

Que vaut le discriminant
(Il va y avoir des simplifications)
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: équations bicarrées
Tout a l'heure j'ai déjà essayer avec le discriminant pour ensuite pouvoir simplifier mais ça marche pas.. Si je n'ai pas d'erreur
Re: équations bicarrées
A mon avis tu as dû te tromper : le résultat est simple : 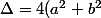^2-4(a^2-b^2 )^2=...) .
.
Si tu as du malà développer, tu peux toujours poser à côté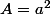 et
et 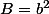

Si tu as du malà développer, tu peux toujours poser à côté

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: équations bicarrées
Ok donc pour le delta j'aurai
4(a²+b²)²-4(a²-b² )² je simplifie les 4 et je fais comme vous dites A=a² et B =b² ce qui fait (A+B )²-(A-B )² au finish je trouve 4AB=4a²b²
4(a²+b²)²-4(a²-b² )² je simplifie les 4 et je fais comme vous dites A=a² et B =b² ce qui fait (A+B )²-(A-B )² au finish je trouve 4AB=4a²b²
Re: équations bicarrées
Voilà, donc ce n'est pas si compliqué que ça 
Quel est le signe du discriminant ? Déduis-en la (ou les) solutions

Quel est le signe du discriminant ? Déduis-en la (ou les) solutions

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: équations bicarrées
Oui enfaite je pensais qu'on va arriver a déterminer a et b et les remplacer dans l'equation
Re: équations bicarrées
Je ne comprends pas ta phrase ; il n'y a rien à remplacer tu as deux solutions (éventuellement confondues) qui s'exprimeront en fonction de  et
et  , c'est tout.
, c'est tout.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: équations bicarrées
zygomatique a écrit:salut
donc en gros tu n'as rien ...
il suffit alors de retourner au collège pour réviser ses identités remarquables ....
et on retourne à nouveau au collège pour réviser ses identités remarquables ...
ton énoncé est incomplet : qu'est-il dit au sujet de a et b ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 46 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
