équation d'une^parabole à partir de 3 tangentes
23 messages
- Page 1 sur 2 - 1, 2
équation d'une^parabole à partir de 3 tangentes
Bonjour
Ce problème à peut-être déjà était posé sur ce forum mais en voici l'énoncé :
on a 3 droites :
y=x
y=-5x+3
y=7x-9
on recherche l'équation d'une parabole qui aurai pour tangentes ces droites
J'ai déjà cherché sur différents sites mais soit les explications n'était pas assez développer et détaillé soit je n'arrivais pas à comprendre car trop compliqué, donc pouvez vous me donner une méthode ou une piste à suivre. Cela fait depuis le début des vacances que je me casse les dents dessus sans pouvoir arriver à démarrer.
merci d'avance
Ce problème à peut-être déjà était posé sur ce forum mais en voici l'énoncé :
on a 3 droites :
y=x
y=-5x+3
y=7x-9
on recherche l'équation d'une parabole qui aurai pour tangentes ces droites
J'ai déjà cherché sur différents sites mais soit les explications n'était pas assez développer et détaillé soit je n'arrivais pas à comprendre car trop compliqué, donc pouvez vous me donner une méthode ou une piste à suivre. Cela fait depuis le début des vacances que je me casse les dents dessus sans pouvoir arriver à démarrer.
merci d'avance
Bonsoir
il faut tenir compte du fait que les points d'abscisses u,v et w sont sur la parabole
au² + bu + c = av² + bv + c
d'ou a(u²-v²) + b(u-v) = 0 et comme u est supposé different de v
a(u-v) + b = 0
d'autre part on a 2au +b = 1 et 2av +b = -5
d'ou 2a(u-v) = 6
ce qui
permet de determiner b
....
même chose en prenant deux autres tangentes, d'ou a
......
il faut tenir compte du fait que les points d'abscisses u,v et w sont sur la parabole
au² + bu + c = av² + bv + c
d'ou a(u²-v²) + b(u-v) = 0 et comme u est supposé different de v
a(u-v) + b = 0
d'autre part on a 2au +b = 1 et 2av +b = -5
d'ou 2a(u-v) = 6
ce qui
permet de determiner b
....
même chose en prenant deux autres tangentes, d'ou a
......
zygomatique a écrit:salutdonc
y = x = u + 1(x - u) donc f(u) = u et f'(u) = 2au + b = 1
y = -5x + 3 = -5(x - v) + 3 - 5v donc f(v) = 3 - 5v et f'(v) = 2av + b = -5
y = 7x - 9 = 7(x - w) + 7w - 9 donc f(w) = 7w - 9 et f'(w) = 2aw + b = 7
.....
dac et en gros à partir de f'(u) f'(v) et f'(w) je peut trouver f(x) ?
marko73 a écrit:dac et en gros à partir de f'(u) f'(v) et f'(w) je peut trouver f(x) ?
on y arrive en écrivant que 3 discriminants sont nuls.
Un seul point d'intersection de la parabole avec la droite y=x
y=ax²+bx+c
y=x
donc
ax²+(b-1)x+c=0
(b-1)²-4ac=0
pareil avec les deux autres droites
Le calcul est assez simple
bonjour
c'est normal tu ne peux pas determiner 6 inconnues a,b,c,u,v et w a partir de 3 equations
il te faut 3 equations supplementaires:
le point de contact de la tangente est sur la parabole, donc
y = u= au^2+bu +c
y = -5v+7 = av^2 + bv+ c
....
remarque
la solution proposee par Chan79 conduit sans doute a des calculs plus simples
alexis6 a écrit:J'ai fait la même chose que zygomatique, mais en enlevant les a et les b, je trouve u=v=w=0, ce qui est impossible...
c'est normal tu ne peux pas determiner 6 inconnues a,b,c,u,v et w a partir de 3 equations
il te faut 3 equations supplementaires:
le point de contact de la tangente est sur la parabole, donc
y = u= au^2+bu +c
y = -5v+7 = av^2 + bv+ c
....
remarque
la solution proposee par Chan79 conduit sans doute a des calculs plus simples
.... bon j'ai pris un crayon et un papier cette fois ...
en espérant ne plus avoir fait de faute ...
c'était aussi pour répondre à siger :: on a six inconnues .... et six équations ...
donc si je n'ai pas fait d'erreur alors j'ai bon comme dirait le seigneur de La Palice ....
:ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
zygomatique a écrit:
.... bon j'ai pris un crayon et un papier cette fois ...
en espérant ne plus avoir fait de faute ...
c'était aussi pour répondre à siger :: on a six inconnues .... et six équations ...
donc si je n'ai pas fait d'erreur alors j'ai bon comme dirait le seigneur de La Palice ....
:ptdr:
" Le calcul est assez simple "
La modestie s'apprend par la répétition de l'échec.
salut
avec les trois discriminants nuls:
ax²+bx+c=x s'écrit ax²+(b-1)x+c=0 et on a (b-1)²=4ac (1)
ax²+bx+c=-5x+3 s'écrit ax²+(b+5)x+(c-3)=0 et on a (b+5)²=4ac-12a (2)
ax²+bx+c=7x-9 s'écrit ax²+(b-7)x+(c+9)=0 et on a (b-7)²=4ac+36a (3)
Dans (2) et (3), on remplace 4ac par b²-2b+1
b²+10b+25=b²-2b+1-12a
b²-14b+49=b²-2b+1+36a
après simplification
a+b=-2
3a+b=4
a=3
b=-5
et c=3
f(x)=3x²-5x+3
avec les trois discriminants nuls:
ax²+bx+c=x s'écrit ax²+(b-1)x+c=0 et on a (b-1)²=4ac (1)
ax²+bx+c=-5x+3 s'écrit ax²+(b+5)x+(c-3)=0 et on a (b+5)²=4ac-12a (2)
ax²+bx+c=7x-9 s'écrit ax²+(b-7)x+(c+9)=0 et on a (b-7)²=4ac+36a (3)
Dans (2) et (3), on remplace 4ac par b²-2b+1
b²+10b+25=b²-2b+1-12a
b²-14b+49=b²-2b+1+36a
après simplification
a+b=-2
3a+b=4
a=3
b=-5
et c=3
f(x)=3x²-5x+3
chan79 a écrit:salut
avec les trois discriminants nuls:
ax²+bx+c=x s'écrit ax²+(b-1)x+c=0 et on a (b-1)²=4ac (1)
ax²+bx+c=-5x+3 s'écrit ax²+(b+5)x+(c-3)=0 et on a (b+5)²=4ac-12a (2)
ax²+bx+c=7x-9 s'écrit ax²+(b-7)x+(c+9)=0 et on a (b-7)²=4ac+36a (3)
Dans (2) et (3), on remplace 4ac par b²-2b+1
b²+10b+25=b²-2b+1-12a
b²-14b+49=b²-2b+1+36a
après simplification
a+b=-2
3a+b=4
a=3
b=-5
et c=3
f(x)=3x²-5x+3
en gros tu me dit que j'ai encore merdé !!! :ptdr:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
bon cette fois ça marche ... j'ai fait deux fois la même erreur que sa majesté m'avait indiqué .... nom d'une pipe en terre cuite ...
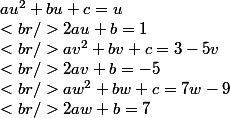
 = 3 \\<br />aw^2 - c = 9 \\<br />a(u - w) = -3)
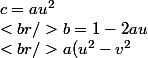 = 3 \\<br />a(u - v) = 3 \\<br />a(u^2 - w^2) = -9 \\<br />a(u - w) = -3)
 = 3 \\<br />u + w = 3 \\<br />2u - v - w = 0)

.... et j'ai repris un crayon et un papier cette fois ...
j'ai cependant fais une opération invalide ... qui la détectera ?
.... et j'ai repris un crayon et un papier cette fois ...
j'ai cependant fais une opération invalide ... qui la détectera ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
chan79 a écrit:salut
avec les trois discriminants nuls:
ax²+bx+c=x s'écrit ax²+(b-1)x+c=0 et on a (b-1)²=4ac (1)
ax²+bx+c=-5x+3 s'écrit ax²+(b+5)x+(c-3)=0 et on a (b+5)²=4ac-12a (2)
ax²+bx+c=7x-9 s'écrit ax²+(b-7)x+(c+9)=0 et on a (b-7)²=4ac+36a (3)
Dans (2) et (3), on remplace 4ac par b²-2b+1
b²+10b+25=b²-2b+1-12a
b²-14b+49=b²-2b+1+36a
après simplification
a+b=-2
3a+b=4
a=3
b=-5
et c=3
f(x)=3x²-5x+3
en gros je comprend le principe mais je ne comprend pas pourquoi pour les discriminant tu trouve (b+5)²=4ac-12a
(b-7)²=4ac+36a
moi je trouve bien (b+5)² -4ac et (b+5)²-4ac puis je passe -4ac de l'autre coté de l'équation comme toi mais je ne comprend pas d'où sort -12a et +36a. Peut tu m'éclairé ?
marko73 a écrit:en gros je comprend le principe mais je ne comprend pas pourquoi pour les discriminant tu trouve (b+5)²=4ac-12a
(b-7)²=4ac+36a
moi je trouve bien (b+5)² -4ac et (b+5)²-4ac puis je passe -4ac de l'autre coté de l'équation comme toi mais je ne comprend pas d'où sort -12a et +36a. Peut tu m'éclairé ?
ax²+bx+c=-5x+3 s'écrit ax²+(b+5)x+(c-3)=0
le discriminant est (b+5)²-4a(c-3)
il doit être nul (sinon il y aurait deux points d'intersection)
(b+5)²-4a(c-3)=0
(b-5)²-4ac+12a=0
Avec cette méthode, à la fin, il faut vérifier les solutions.
chan79 a écrit:ax²+bx+c=-5x+3 s'écrit ax²+(b+5)x+(c-3)=0
le discriminant est (b+5)²-4a(c-3)
il doit être nul (sinon il y aurait deux points d'intersection)
(b+5)²-4a(c-3)=0
(b-5)²-4ac+12a=0
Avec cette méthode, à la fin, il faut vérifier les solutions.
Dac là je vien de pigé merci beaucoup. Ta méthode est plus simple à comprendre que celle de zygomatique
23 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 69 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
