Equation du troisième degré :

[P130]

:happy2: Bonjour à tous.

Je suis en train de préparer un contrôle et il faudrait que je révise les équations du 3ème degré : Seule problème, j'ai rien compris :hum: !

Le prof à beau m'expliquer cinquante fois, ça rentre pas ! ( Faut dire qu'il esplique pas très bien : On l'a juste vu au cours d'un exo et maintenant on est censé savoir le faire ) :marteau:

Donc si qqun avait l'extrème amabilité de me faire un petit topo ( comment on les résoud, etc ...) sur le sujet je serais extrèmement heureux ! :we:

Merci d'avance :id:

[Sphinx]

Mais ma parole qu'est-ce qu'on vous apprend à l'école?
A l'époque,c'était plus tard ces équations-là!
Bon si tu as une équation du type ax^3+bx^2+cx+d=0,tu dois te ramener à une équation du type x^3+px+q=0(trouve un moyen de te débarrasser du x^2,par exemple en mettant sous forme canonique(ax^3+bx^2 est le début d'un cube...))
Soit tu connais les formules de Cardan,soit non.
Dans ce cas pose x=u+v.
Normalement ça te ramène à une équation du second degré où tu dois trouver u^3 et v^3.
En effet (u+v)^3+p(u+v)+q=u^3+v^3+3uv(u+v)+p(u+v)+q=0
Donc u^3+v^3+q=0 et 3uv+p=0
Donc uv=-p/3 et donc u^3*v^3=-p^3/27
Alors u^3+v^3=-q et u^3*v^3=-p^3/27
Ceci te fournit une équation du second degré où tu dois trouver u^3 et v^3 connaissant leur somme(-q) et leur produit(-p^3/27).
Quand tu as u^3 et v^3,tu as automatiquement u et v et donc x=u+v.
Attention tout de même à prendre les solutions convenables.Théoriquement il y a toujours 3 solutions réelles si les coefficients a,b,c,d sont réels.
Bonne continuation!
Ciao!

[Mikou]

hum je pense qu'il ya un pb la. La resolution des equations de degres 3 n'est en rien exigible en Term S, par contre elle peut etre abordée pour l'intelligence de la méthode et/ou pour introduire les complexes, je parle bien sur de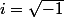
Je crois que tu parlais des equations de degres 3 ou il ya une racine évidente dans lequel cas tu peux utiliser la factorisation et retomber sur un polynome de degres 2. La derniere chose qui me vient a l'esprit est lutilisation de la derivation puis d'utiliser le théoreme de la bijection ( sur les differents intervalles ) et de conclure quant nb de racines ainsi que de donner des valeures approchées.

[fonfon]

Salut, je pense que c'est plutôt ce que mikou a dit sinon ca me parait bizzare que l'on demande de resoudre des equations du 3eme degres c'est que la term a vraiment evolué

[Frangine]

Quand on interroge son profil on voit qu'il est en 1ère S.
Donc les seules équations du 3ème degré qu'on peut lui poser sont celles qui ont une racine évidente x1 et on les guide pour mettre (x - x1) en facteur

par exemple

Soit P le polynôme défini par P (x) = 6 x^3 + x^2 – 4 x + 1

1 ) On pose Q (x) = ( 3 x – 1 ) ( a x^2 + b x + c )
Développer Q (x) = 3 a x^3 + x^2 (3 b – a ) + x (3 c – b) – c

2 ) Déterminer a , b et c tels que, pour tout réel x, P (x) = Q (x)
Dire que , pour tout réel x, P (x) = Q (x) revient à dire que :

3 a = 6
3b – a = 1
3 c – b = – 4
– c = 1

on trouve a = 2 et b = 1 et c = – 1

Ainsi pour tout réel x, on a :
P (x) = ( 3 x – 1 ) ( 2 x^2 + x –1 ) ce qui est plus simple à résoudre que sous la forme initiale

[P130]

voila c'est avec une recine évidente ! Désolé j'aurais du le préciser. Merci à Frangine et merci quand mêmes aux autres.

Bon je vais voir ça , merci à tous :king2:

[P130]

ok merci j'ai bien capté le truc mais ya quand meme quelquechose que je n'ai pas compris :

Pourquoi ( 3x - 1 ) en facteur ( enfin, surtout pk 3 ??!) :mur:

[fonfon]

ok merci j'ai bien capté le truc mais ya quand meme quelquechose que je n'ai pas compris :

Pourquoi ( 3x - 1 ) en facteur ( enfin, surtout pk 3 ??!)

on met en facteur (3x-1) car 1/3 est racine de ton polynôme donc tu aurais pu mettre (x-1/3) en facteur c'est parce que ca elimine la fraction

[P130]

a oui ok !! merci bien :we: