DM - "Equation du troisième degré à coefficients réels"

[Pascal le nain]

Bonjour,

A peine avons-nous commené l'année que notre prof nous colle un DM sur un sujet qu'on a jamais vu, bref le bordel. Voila l'énoncé :
dans l'énoncé, un C majuscule signifie "appartient"


1. Soit 1'equation : X3 + aX2 + bX + c = 0 (1) a coefficients a, b et c réels et d'inconnue
X réelle. On pose X = x + (x et C R). Quelle valeur faut-il donner à pour que l'équation en x qu'on obtient n'ait pas de termes en x2 ?

je me suis dis que = x - 1 donc on a 1 + a + b + c = 0. Mais la suite ne me conforte guère dans mon idée...


On se ramène donc a 1'equation : x3 + px + q = 0 (2) . Exprimer p et q en fonction de a, b et c.
2. Montrer que pour tout réel et tout réel , il existe, sous des conditions que l’on précisera,
deux réels, éventuellement égaux, u et v tels que

u + v =
u.v =

3. Pour résoudre 1'equation (2) on pose x = u + v avec u.v = -p/3 . Montrer que (2) conduit à
la résolution du système.
u³ + v³ = -q
u³.v³ = - p³/27 (3)
u.v C R

En déduire que u3 et v3 sont les solutions d'une équation du deuxième degré dont on calculera le discriminant. Soit une des racines carrées de ce discriminant, exprimer u3 et v3 en fonction de q et . u et v sont alors des racines cubiques de ces nombres.
4. Appliquer cette méthode à 1'équation suivante :
• x3 + 3x2 + 15z + 76 = 0
5. Appliquer cette méthode aux équations suivantes en utilisant 1'extension des nombres réels
aux nombres complexes et 1'indication fournie : • x3 — 12x — 8\/(2) = 0 (pour cette équation on
calculera préalablement le cube de — V2 — iV(2))
• x3 — I5x — 4 = 0 (pour celle-ci on calculera d'abord le cube de 2 — i).

[B_J]

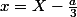
Pour resoudre une equation du type on pose et on obtient une equation du type
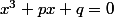
Indice : dans l'equation de depart remplace par

[B_J]

Bonjour,



je me suis dis que = x - 1 donc on a 1 + a + b + c = 0. Mais la suite ne me conforte guère dans mon idée...

doit etre independant de x !

[B_J]

maintenant , il faut remarquer que l'equation admet au moins une racine reelle (on peut appliquer le theoreme des valeurs intermediaires ou remarquer que dans , l'equation admet trois racines complexes et comme ses coefficients sont reels alors si est solution , son conjugué l'est aussi donc il y'a au moins une racine reelle )

[B_J]

maintenant remarque que et sont racine de
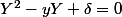
d'ou les conditions sur u et v ( pour que cette equation du 2nd degré admette des racines reelles

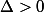
[B_J]

si tu as des pb pour la suite , n'hesites pas a demander :we:

[Pascal le nain]

lol t'es déjà trop compliqué là :ptdr:

je sais absolument rien de la manière de faire cet exo, la prof nous a donné ce truc alors qu'on fais le résonnement par récurence en cours.

Soit plus précis s'il te plait :marteau:

dsl

[B_J]

y'a pas de recurrence ici
sinon avec google tape :
equation troisieme degré
ou
cardan
tu trouveras ce que tu cherches
PS: t en quelle classe ( quel niveau) ?

[Pascal le nain]

Ok c'est bon j'ai trouvé :id:

ps : je suis rentré en TS :hein: