Equation trigonometrique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
marc1998
- Messages: 4
- Enregistré le: 26 Aoû 2015, 10:30
-
 par marc1998 » 31 Aoû 2015, 11:15
par marc1998 » 31 Aoû 2015, 11:15
Coucou les gens

Alors j'ai un exercice sur les equations trigo et je broque dessus,
ca donne:
sin(3x+ pi/4) = sqrt(3)/4
je crois comprendre qu'il faut remplacer sqrt(3)/4 par sin(pi/3) pour pouvoir enlever les "sin" des deux coté de l'equation puis isoler le x ensuite mais mon resultat donne x= pi/36 et sachant que cela se deroule sur l'intervalle ]-pi ; pi[*cela fait beaucoup de solutions...
Pouvez vous m'aider ? Merci ^^
-
mathelot
 par mathelot » 31 Aoû 2015, 11:25
par mathelot » 31 Aoû 2015, 11:25
 n
n'est
pas une valeur remarquable.
mon conseil
développe
)
fais passer la racine de 2 à droite du signe égal
élève (sin(3x)+cos(3x)) au carré , ce qui permet de résoudre en inconnue sin(6x)
-
mathelot
 par mathelot » 31 Aoû 2015, 11:35
par mathelot » 31 Aoû 2015, 11:35
marc1998 a écrit: sin() = sqrt(3)/4
ou alors ton parenthèsage est faux et il faut lire
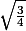
-
marc1998
- Messages: 4
- Enregistré le: 26 Aoû 2015, 10:30
-
 par marc1998 » 31 Aoû 2015, 11:39
par marc1998 » 31 Aoû 2015, 11:39
mince dsl j'ai fait une faute de frappe c'est pas sqrt(3)/4 mais sqrt(3)/2, cependant est ce que cela change beaucoup au fait que se soit une valeur remarquable ?
-
mathelot
 par mathelot » 31 Aoû 2015, 11:42
par mathelot » 31 Aoû 2015, 11:42
marc1998 a écrit:mince dsl j'ai fait une faute de frappe c'est pas sqrt(3)/4 mais sqrt(3)/2, cependant est ce que cela change beaucoup au fait que se soit une valeur remarquable ?
oui, ça simplifie beaucoup.
l'équation s'écrit
=sin(\frac{\pi}{3}))
-
marc1998
- Messages: 4
- Enregistré le: 26 Aoû 2015, 10:30
-
 par marc1998 » 31 Aoû 2015, 11:47
par marc1998 » 31 Aoû 2015, 11:47
d'accord, et est ce que les sin doivent s'annuler ensuite ? ou je dois réunir sin(pi/4) et sin(pi/3) ?
-
mathelot
 par mathelot » 31 Aoû 2015, 11:55
par mathelot » 31 Aoû 2015, 11:55
mathelot a écrit:oui, ça simplifie beaucoup.
l'équation s'écrit
=sin(\frac{\pi}{3}))
On cherche deux arguments réels sur le cercle qui ont même sinus.
Faire un dessin , noter
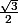
sur l'axe y'oy et "remonter" cette ordonnée
sur le cercle en deux points

et

-
mathelot
 par mathelot » 01 Sep 2015, 15:46
par mathelot » 01 Sep 2015, 15:46

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 01 Sep 2015, 17:00
par zygomatique » 01 Sep 2015, 17:00
marc1998 a écrit:mince dsl j'ai fait une faute de frappe c'est pas sqrt(3)/4 mais sqrt(3)/2, cependant est ce que cela change beaucoup au fait que se soit une valeur remarquable ?
salut
 = \dfrac {\sqrt 3} 4)
(1)

donc il existe un réel u tel que
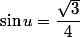
donc
 3x + \dfrac \pi 4 = u + k2\pi \ ou \ 3x + \dfrac\pi 4 = \pi - u + k2\pi ...)
puis on résout chacune des équations pour avoir x en fonction de u (dont on peut donner une valeur approchée si on veut)
le fait d'avoir "une valeur remarquable" permet simplement de donner une valeur exacte à u ... mais la résolution est en tout point identique ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 75 invités
