équation trigonométrique rapide
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 20:46
par Bertrand Hamant » 17 Sep 2005, 20:46
Bonjour je dois démontrer que pour tout réel x :
cos x + sin x = V2 cos ( x - Pi / 4 )
j'ai developpé V2 cos ( x - Pi / 4 ) =
V2[ cos x cos ( Pi / 4 ) + sin x sin ( Pi / 4 )] = V2 [ V2 / 2 ( cos x + sin x ) ]
soit après simplification on obtient bien cos x + sin x = V2 cos ( x - Pi / 4 )
J'aimerais connaitre votre confirmation merci
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 21:09
par Bertrand Hamant » 17 Sep 2005, 21:09
J'aimerais savoir si ma méthode est bonne ou pas merci
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 17 Sep 2005, 21:14
par cesar » 17 Sep 2005, 21:14
Bertrand Hamant a écrit:Bonjour je dois démontrer que pour tout réel x :
cos x + sin x = V2 cos ( x - Pi / 4 )
cos(pi/4) = sin(pi/4) = 1/racine(2)
donc
cos(x) *1/racine(2) + sin(x)* 1/racine(2) = cos(x -pi/4)
grace à la formule :
cos(a-b) =cos(a)*cos(b) + sin(a)*sin(b) ici a= x et b=pi/4
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 21:16
par Bertrand Hamant » 17 Sep 2005, 21:16
J'aimerais savoir si la méthode que j'ai employée au début est bonne ou pas merci de votre confirmation
j'ai utilisé la formule cox ( a - b ) et après simplification j'ai eu cos x + sin x
merci de me confirmer
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 17 Sep 2005, 21:25
par N_comme_Nul » 17 Sep 2005, 21:25
Salut !
Si seule la réponse à ta question t'intéresse, alors c'est oui.
-
cesar
- Membre Rationnel
- Messages: 841
- Enregistré le: 05 Juin 2005, 07:12
-
 par cesar » 17 Sep 2005, 21:26
par cesar » 17 Sep 2005, 21:26
c'est bien une confirmation que j'ai fait, sauf que j'ai cité la relation utilisée, ce que je te conseille de faire, car la demo n'est pas tout à fait évidente "à froid"
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 21:29
par Bertrand Hamant » 17 Sep 2005, 21:29
Merci beaucoup de votre confirmation. Oui en effet je la mettrai cesar merci pour cette subtilité. Quant à Nul, je te suis reconnaissant d'avoir utilisé une autre manière. Cependdant je sais que cos ( x - Pi / 2 ) = sin x
mais la suite je ne comprends pas comment tu as fais avec x + x. Merci encore
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 17 Sep 2005, 21:48
par N_comme_Nul » 17 Sep 2005, 21:48
Resalut !
J'ai utilisé une formule de trigo qui permet de transformer la somme de deux fonctions cosinus en un produit :
pour tous réels

et

:
[CENTER]
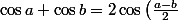\cos\left(\frac{a+b}{2}\right))
[/CENTER]
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 22:06
par Bertrand Hamant » 17 Sep 2005, 22:06
est ce possible de résoudre
cos x + sin x = 2
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 17 Sep 2005, 22:12
par N_comme_Nul » 17 Sep 2005, 22:12
Salut !
Pour tout réel

:

et

donc

A voir ça ... on dirait que ça pourrait exister ... mais en fait ... :hum:
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 22:15
par Bertrand Hamant » 17 Sep 2005, 22:15
j'essaye de chercher mais je ne trouve pas
on sait que le sinus et le cosinus sont compris entre 0 et 1, j'en déduis qu'il n'y pas de solutions, est ce possible
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 17 Sep 2005, 22:25
par N_comme_Nul » 17 Sep 2005, 22:25
Je te propose d'étudier la fonction
=\cos x+\sin x)
de dérivée
=\sqrt2\cos\left(x+\frac{\pi}{4}\right))
En étudiant le signe de ça sur
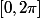
(

est

-périodique), on trouve que les extrema sont atteints en
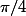
et

.
Reste à calculer les valeurs de

en ces points ...
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 22:35
par Bertrand Hamant » 17 Sep 2005, 22:35
Ils valent - 2 pour x = pi / 4 et 5 pi /4
j'avais trouvé
mais comment résoudre cos x + sin x = 2
on sait que V2 cos ( x - pi / 4 ) = 2
donc
on a cos ( x - Pi / 4 ) = V 2
soit
x = Pi / 4
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 17 Sep 2005, 22:42
par N_comme_Nul » 17 Sep 2005, 22:42
Je ne suis pas d'accord avec toi :
on trouve
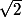
et

respectivement pour

et

.
D'autre part, j'ai montré (sans les détails) que

-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 22:52
par Bertrand Hamant » 17 Sep 2005, 22:52
voici comment j'ai fait
on sait aussi que V2 cos ( x - PI/4 ) = 2
ce qui équivaut à cos ( x - PI/4 ) = V2
-
N_comme_Nul
- Membre Relatif
- Messages: 127
- Enregistré le: 06 Aoû 2005, 22:00
-
 par N_comme_Nul » 17 Sep 2005, 22:58
par N_comme_Nul » 17 Sep 2005, 22:58
"ce qui équivaut à cos ( x - PI/4 ) = V2"
Ok :D j'ai "percuté". :marteau:
cosinus étant inférieur ou égal à 1, et racine de 2 supérieur à 1, l'équation est impossible :++:
-
Bertrand Hamant
- Membre Rationnel
- Messages: 618
- Enregistré le: 02 Sep 2005, 14:14
-
 par Bertrand Hamant » 17 Sep 2005, 22:58
par Bertrand Hamant » 17 Sep 2005, 22:58
voici comment j'ai fait
on sait aussi que V2 cos ( x - PI/4 ) = 2
ce qui équivaut à cos ( x - PI/4 ) = V2
on sait que cos ( Pi / 2 - x ) = sin x
soit 2 cos ( x - Pi / 2 ) = V 2
soit donc sin x = V2/ 2
x = Pi / 4
avec l'intervalle en dessous on a aussi 5 pi / 4
que penses tu de cette méthode Nul
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
