Equation - Terminal S

[and1dx]

Bonsoir,

Pourriez vous me donner une indication pour resoudre:




Merci

[Mortelune]

Bonjour, si tu as vu les formules d'euler (avec les exponentielles complexes) on doit pouvoir s'en sortir.

[Arnaud-29-31]

Salut,
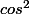
Ca m'a l'air costaud comme calcul, tu es sur que tu as bien recopié ? (genre c'est pas à la fin plutôt que ?)

[Mortelune]

Bonjour, oui parce que même en bourrinant avec de l'exponentielle complexe je sèche, il y a aucune simplification.

edit : Et pareil avec logiciel de calcul formel, il trouve que des trucs moches ^^

[and1dx]

Je pense aussi que c'est du cos^2(x) a la fin mais l'enonce est formé comme je l'ai ecrit dans le message précèdent.

[Mortelune]

C'est l'énoncé d'un problème ou seulement un exercice ?
Dans le premier cas la question est-elle cohérente avec la suite ? dans le second cas résous avec un ² à la fin, personne n'est à l'abri d'une coquille dans l'énoncé.

[and1dx]

Non c'est un énoncé merci quand meme je vais essayer avec le ² :)

[and1dx]

C'est bon avec le ca se fait

[Black Jack]

Tout dépend du but de l'exercice.
Veut-on trouver les solutions exactes ou bien des solutions approchées sont-elles suffisantes ?
Si on est dans ce cas, une simple étude de fonction montre qu'il y a 4 solutions (à 2k.Pi près) qu'on peut trouver par approximations successives avec la précision qu'on veut (sauf les valeurs exactes).

On trouve alors comme solutions :

-2,1972... + 2k.Pi
0,2512... + 2k.Pi
0,8353... + 2k.Pi
2,9617... + 2k.Pi

Avec k dans Z
********

Si par contre le cos³(x) devient cos²(x) dans l'équation de départ, alors ...

L'équation peut se transformer en cos(2x) + V3.sin(2x) - V3 = 0

Et sauf erreur, on trouve alors :
x = Pi/4 + k.Pi
OU
x = Pi/12 + k.Pi
Avec k dans Z
********
Mais je suis souvent distrait.

:zen: