Equation

[Gagnantdu06]

Bonsoir

1.La parabole P ci-dessous représente la fonction f définie sur R par f(x)= (x+3)(x-1).
Utilisez la courbe pour résoudre graphiquement dans R:
a)l'équation x² + 2x - 3 = 0
b)l'inéquation x² + 2x - 3 0

2.Vérifiez que l'équation (E): x² + 2x + 4 = 0 équivaut à f(x) = -7
Déduisez-en l'ensemble des solutions de (E).


Je sais que vous n'avez pas la courbe devant les yeux, désolé en ce moment je ne peux pas faire de screen.
Mais pouvez-vous me dire ce qu'il faut faire car là je sèche vraiment, à court d'idée ( je parle surtout pour la a) et b) )
Vous pouvez à peu près connaitre la courbe car c'est une parabole descendant en passant par -3 en abscisse et remontant en 1 en abscisse.

[Timothé Lefebvre]

Salut, nous aussi nous avons des caltos graphiques ne t'en fais pas.

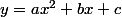
Pour tes équa et inéqua rappelle-toi que c'est de la forme ou etc...
Tu connais a, b et c et tu déduis y et x de la courbe, voilà.

[Gagnantdu06]

J'avais compris sa xd mais je vois pas comment faire.

[Timothé Lefebvre]

Tu utilises les coordonnées de plusieurs points pour faire un système d'équations !

Tu as développé l'expression de f(x) bien sûr ?

[Gagnantdu06]

ué j'ai développé x² - x + 3x - 3 = x² + 2x -3
mais je vois pas comment faire tout de meme xd.
J'ai bien compris qu'il fallait faire un système dès le début mais lequel xd.

[Timothé Lefebvre]

Si tu veux pas te faire c*** tu fais :





Produit de facteurs nul.

[Tu peux qussi vérifier en résolvant le trinôme]

Pour ton exo il s'agit de prendre les coordonnées (x,y) de trois points, de les mettre en système et de résoudre ! Pour y=0, x = ... et voilà !

[SimonB]

Pour ton exo il s'agit de prendre les coordonnées (x,y) de trois points, de les mettre en système et de résoudre ! Pour y=0, x = ... et voilà !

Non. Il s'agit de lire graphiquement les solutions.

En l'occurence, de trouver les points où la courbe croise l'axe des abscisses (pourquoi ?).

[Timothé Lefebvre]

En l'occurence, de trouver les points où la courbe croise l'axe des abscisses (pourquoi ?).

Ben vu la valeur de y avec laquelle on bosse ...

[SimonB]

Ben vu la valeur de y avec laquelle on bosse ...

Je sais que toi tu le sais, c'était plus un questionnement pédagogique...

[Gagnantdu06]

La courbe croise l'axe des abscisse en -3 et en 1
Mais après comment expliquer pourquoi?

[Timothé Lefebvre]

Pourquoi ? Car tu le vois.

Pourquoi faire ça ? Parce qu'on cherche les valeurs de x pour y = 0 donc quand la courbe coupe l'axe des abscisses.

Tu comprends ?

[Gagnantdu06]

alors après on cherche les valeurs qui sont inférieurs ou égal à 0 (donc un intervalle)?
S=[-3;1]
est ce cela?
et pour la 2 eme question que faut il faire?

[SimonB]

Pourquoi faire ça ? Parce qu'on cherche les valeurs de x pour y = 0 donc quand la courbe coupe l'axe des ordonnées.

Des abscisses !

Pour l'inégalité <0 : de la même manière, il faut chercher les abscisses des points où la courbe est en-dessous de l'axe des abscisses.

[Timothé Lefebvre]

Des abscisses !

Pour l'inégalité <0 : de la même manière, il faut chercher les abscisses des points où la courbe est en-dessous de l'axe des abscisses.

Shit tu as raison, j'ai pas fais attention, mea culpa.

[Gagnantdu06]

je n'arrive pas à résoudre l'équation suivante:
(x+1)²+3 = 0
Merci de votre aide.

EDIT : j'ai fusionné les discussions et fait le ménage pour plus de clarté.

[le_fabien]

Bonsoir,je n'arrive pas à résoudre l'équation suivante:
(x+1)²+3 = 0
Merci de votre aide.

Là cela va être dur de la résoudre celle là!!

[Timothé Lefebvre]

Tu es en quelle classe au fait ?

[Clembou]

Bonsoir,je n'arrive pas à résoudre l'équation suivante:
(x+1)²+3 = 0
Merci de votre aide.

C'est la résolution d'une équation du second degré avec la méthode du discriminant...

Tu es en quel classe ?

[le_fabien]

Tu es en quelle classe au fait ?

Qui moi ?? :ptdr:

[Timothé Lefebvre]

Qui moi ?? :ptdr:

:ptdr: :ptdr:
Je ne pense pas que tu puisse avoir du mal à la résoudre

A part le discriminant ça va être chaud !